The Resonance Mechanism and its Properties
Naveen Durvasula , Maryam Bahrani 1 year ago ↓ PDF
In the last post, we built our way up to a formal definition of the heterogeneous setting. In this post, we formally introduce the Resonance mechanism and outline the desiderata that it provably satisfies. The main idea behind the mechanism that allows it to succeed despite the complexity of the heterogeneous setting is that it introduces a new set of agents: brokers. Brokers are sophisticated and profit-seeking agents that are capable of computing efficient allocations. Resonance is a market mechanism that aligns the incentives of brokers and utilizes their sophistication to generate good market outcomes for users and nodes.
For a deeper dive into the mechanism including full proofs of all theorems we state below, check out the Resonance paper.
A Recap of the Heterogeneous Setting
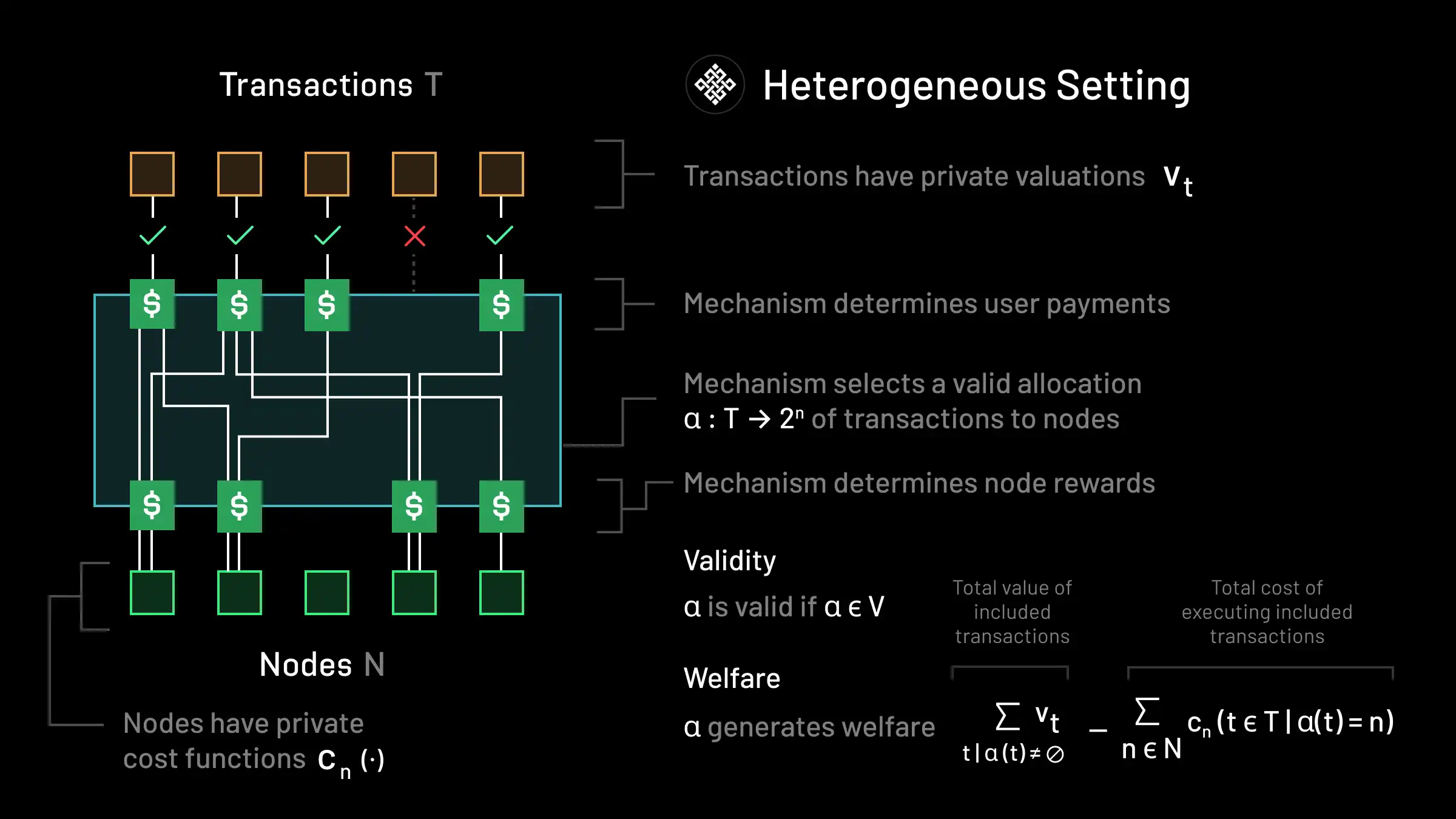
Transactions, Nodes, Valuations, and Costs
As outlined in the previous post, in the heterogeneous setting, there is a set of transactions T and a set of nodes N. For each transaction t∈T, there is a valuation vt∈R≥0 that denotes the maximum amount of money that the user who submitted t is willing to pay to have t be executed. For every node n∈N, there is a cost function cn(X):2T→R≥0 which denotes the amount of money node n must be paid in order to execute a bundle of transactions X⊆T. We require that cn(∅)=0. This cost function is general to allow nodes to have custom costs depending on their hardware, what they can run in parallel, and how they choose to schedule and run the jobs that are assigned to them. Nodes could even be other chains, where costs correspond to transaction fees for execution on that chain. Initially, valuations are only known privately to users submitting transactions, and cost functions are known privately to nodes.
Allocations and Validity
An allocation α:T→2N assigns each transaction to a (possibly empty) set of nodes. The inverse of an allocation α is defined as α−1(n):={t∈T∣n∈α(t)}, which specifies the transactions that a node n executes under the allocation α. Resonance can handle arbitrary allocation validity constraints; this is denoted by enforcing that the mechanism must return an allocation that belongs to a set Vof valid allocations. The only constraint made on V is that the empty allocation that sets α(t)=∅ for all t must lie in the set. This allows it to capture any reasonable execution constraint, e.g.:
- Preventing nodes from exceeding their resource constraints. This is similar to the constraints we saw in all of the previous examples.
- Ensuring that transactions that are allocated to different nodes do not touch the same part of the network state. This is similar to the account constraint we saw in Solana.
- Preventing transactions from running on nodes without the requisite specialized hardware (e.g. GPUs)
- Enabling greater functionality for transactions. For example, we could allow transactions to execute privately by assigning a transaction to multiple nodes concurrently and running a secure multi-party computation scheme
The last two bullets correspond to examples of net-new functionality in our setting that previous fee market designs do not have the capability to price. That is to say, whereas previous settings, including the prover market setting, establish fungible units of computation, in the heterogeneous setting, we allow for arbitrary non-fungible computation. We abstract away these extremely general families of constraints in the heterogeneous setting into a set of valid allocations V that is specified by the protocol. As Ritual develops new functionality, Resonance can automatically price transactions that make use of that functionality by simply modifying V.
Payment Rules and Routings
In addition to finding an allocation, a fee mechanism in the heterogeneous setting must also determine how much each user should pay, and how much each node should receive. A transaction payment rule π:T→R≥0 determines how much each transaction should pay for execution. A node payment rule ϕ:N→R≥0 determines how much each node should be paid for the execution of transactions assigned to it.
A routing (α,π,ϕ) specifies a valid allocation α∈V, and the user and node payment rules. Note that that the definition of routings requires that the allocation is valid. A routing is what we ultimately want our mechanism to return.
Utilities, Welfare, and Surplus
A subtlety in thinking about economic efficiency comes from the nuance between welfare, as discussed in the previous post, and a related notion called surplus. To discuss either, we first need to characterize how different agents obtain utility.
Transactions (Users): Given a routing R=(α,π,ϕ), a user who submits a transaction t obtains positive utility equal to their valuation vt if the transaction is included (i.e. if α(t)=∅), and negative utility equal to the payment they make
Nodes: A node obtains positive utility equal to the rewards they receive, and negative utility equal to the cost for executing the transactions it is assigned
We let v and c denote the full vectors of valuations and cost functions.
Welfare: The social welfare generated by a routing R=(α,π,ϕ) depends only on the allocation α, and is given by the gap between the valuations of included transactions and the costs incurred by nodes executing transactions
Surplus: The surplus generated by a routing R=(α,π,ϕ) depends on the allocation and payment rules, and is given by the sum of the utilities of transactions and nodes
Surplus is very closely related to welfare. We can in fact write surplus in terms of welfare as:
The extracted margin is given by the gap between the total payments made by users and the total payments made to nodes. In the desiderata we establish below, we would like a fee mechanism that maximizes surplus rather than just welfare. That is, it should not only maximize welfare, but also ensure that there is no extracted margin; we would ideally like all of the value generated by the mechanism to flow to users and nodes, instead of being captured by some other party.
Desiderata
Now that we have established the setting, we informally outline the desiderata that we would like a fee mechanism to obtain:
- Budget-Balance: The mechanism should not require subsidization to run.
- Individual Rationality: No one is worse off by participating in the mechanism than abstaining. That is, all utilities are non-negative.
- Efficiency: The mechanism finds a surplus-maximizing routing. Again, this differs from the concept of welfare that we described in the previous section.
- Incentive-Compatibility: The mechanism is ex-post incentive compatible, meaning truth-telling by users and nodes is a Nash equilibrium. This property leads to a simple UX, where users do not need to strategize to obtain good outcomes.
- Tractability: The mechanism is computationally lightweight and feasible to implement on-chain.
The Resonance Mechanism
Introducing Brokers
The key idea that allows Resonance to obtain good performance in this setting, despite its complexity, is to introduce an entirely new set B of agents: brokers. Brokers are purely profit-seeking agents that use predictions of transaction demand and supply as well as their own compute resources to find economically efficient allocations of transactions to nodes within the network and payment rules. They can be thought of as spiritually similar to builders in their capabilities; however, unlike in the Ethereum block building process, Resonance provides strong guarantees on the equilibrium behavior of brokers at pure Nash equilibrium.
Mechanism Description
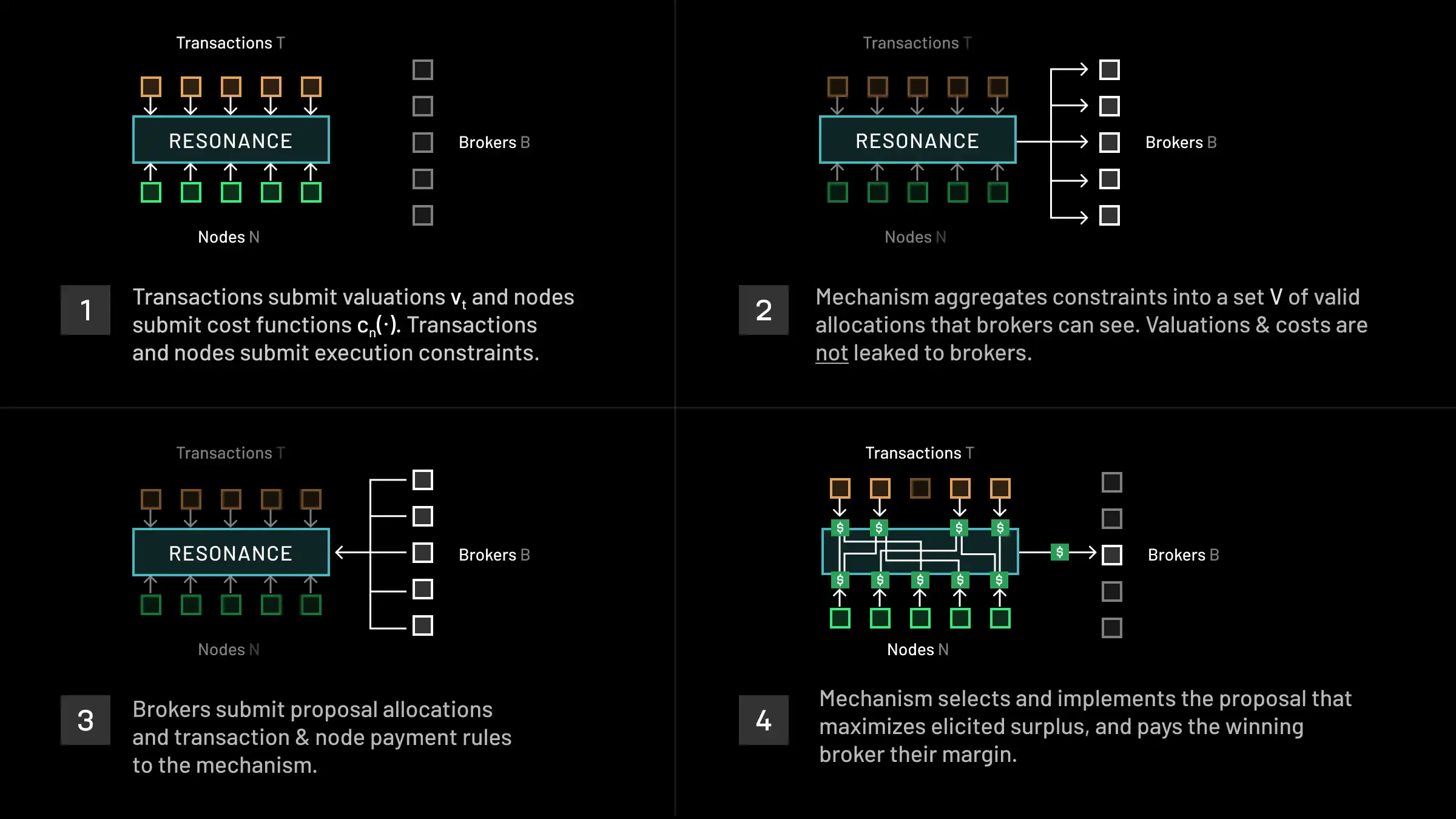
The end-to-end flow of the Resonance mechanism occurs in four steps:
- First, users submit transactions to the mechanism along with their valuations vt for inclusion, and nodes submit their cost functions cn(⋅) to the mechanism. Transactions and nodes must also submit their corresponding constraints. Constraints for nodes may include individualized resource constraints, constraints on available software or data to execute specialized payloads, bandwidth constraints, etc. Constraints for transactions may include restrictions on node specifications or data availability. Transactions using expanded functionality may have even more complex constraints e.g. requiring nodes in a specific geographic region to execute transactions or requesting privacy by means of a multi-party computation scheme involving multiple nodes.
- The mechanism then aggregates those constraints, and adds additional protocol-level ones e.g. preventing state conflicts between transactions that are run on different nodes. The full set of constraints is represented by a set V of valid allocations. The total set of all constraints is broadcast to brokers. Crucially, the valuations and costs that were submitted to the mechanism in the first step are not broadcast or leaked to the brokers.
- Next, each broker b∈B submits a routing Rb=(α,π,ϕ), consisting of a valid allocation α∈V and payment rules π and ϕ. Computing a good routing can be computationally complex and further require good predictions of transaction valuations and node costs. The task is spiritually similar to what builders and searchers do today.
- After receiving the proposals, the mechanism chooses the routing that maximizes elicited surplus. That is, letting v′ and c’ denote the reported vectors of valuations and node cost functions respectively, the mechanism chooses a routing R∗=(α∗,π∗,ϕ∗)∈argmaxb∈BS(Rb∣v’,c’) that maximizes surplus according to v’ and c’. If R∗ does not yield negative utility for any user or node, the mechanism implements R∗ and rewards the winning the broker b∗ who submitted R∗ with the margin of their routing ∑t∈Tπ∗(t)−∑n∈Nϕ∗(n). Otherwise, the mechanism implements the null routing (i.e. no transactions are executed, and nobody pays/receives payment).
The valuations v’ and costs c’ that are reported to the mechanism are used only to compute which broker proposal maximized elicited surplus. The mechanism does not use these values to compute a routing itself because this would lead to (a) violations in incentive compatibility, since lying about one’s valuation or cost could allow one to benefit, and (b) violation of tractability, since computing even an approximately optimal routing given reported valuations and costs may be prohibitively computationally expensive. Brokers must submit proposals without knowing the reported valuations and costs.
Mechanism Analysis
Resonance satisfies all five desiderata. Below we provide intuition for each; formal proofs can be found in Section 3.2 of the Resonance paper.
Budget-balance
Because we restrict brokers to submitting proposals with positive margins, the mechanism is budget balanced.
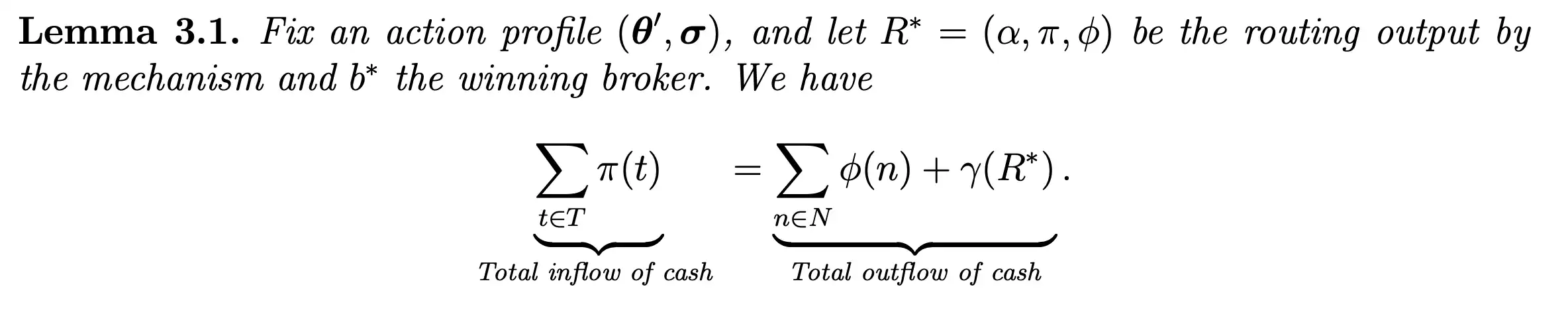
Individual Rationality
The mechanism is individually rational for users and nodes because we prevent proposals that result in negative utility for some user or node from being implemented.

It is also individually rational for brokers.
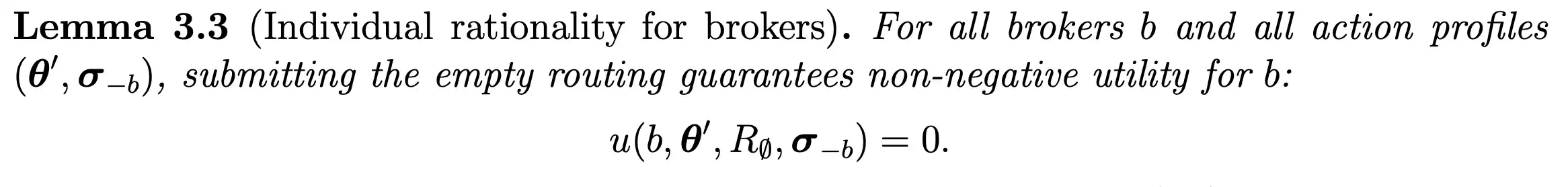
Efficiency
Our discussion of efficiency is slightly more nuanced. Ideally, there are at least two non-colluding brokers who submit competing proposals to the mechanism. In this case, we can prove the below guarantee that shows surplus-maximization at equilibrium:

However, even if there is only one broker (or all brokers collude), the protocol still maximizes welfare at equilibrium, although it no longer maximizes surplus. The one broker can extract the value generated by the routing.

Incentive Compatibility
The mechanism is also incentive compatible for users and nodes at equilibrium.
Tractability
Resonance is simple to describe, and computationally light-weight. The computational steps involve calculating the surplus of each proposal, finding the proposal with maximum surplus, and checking that it results in non-negative utility for all agents. All of these steps can be done in time proportional to (∣T∣+∣N∣)⋅∣B∣ (assuming agent types have constant description size).
Comparison to existing designs
A natural question to ask is whether there is an easy way to generalize the fee markets that have been used in existing settings to the heterogeneous setting. As multi-dimensional fee markets are the most heterogeneous fee markets of the ones described above that have also seen wide-scale adoption, we ask whether a variant of that design can be adapted. Of course, this is somewhat of an apples to oranges comparison, since in the multi-dimensional knapsack setting the mechanism only needs to select a block, whereas in the heterogeneous setting the mechanism needs to select a much richer allocation and set prices for execution nodes as well. Furthermore, without any resource numeraire restricting the space of cost functions, it’s unclear how the mechanism would even be adapted.
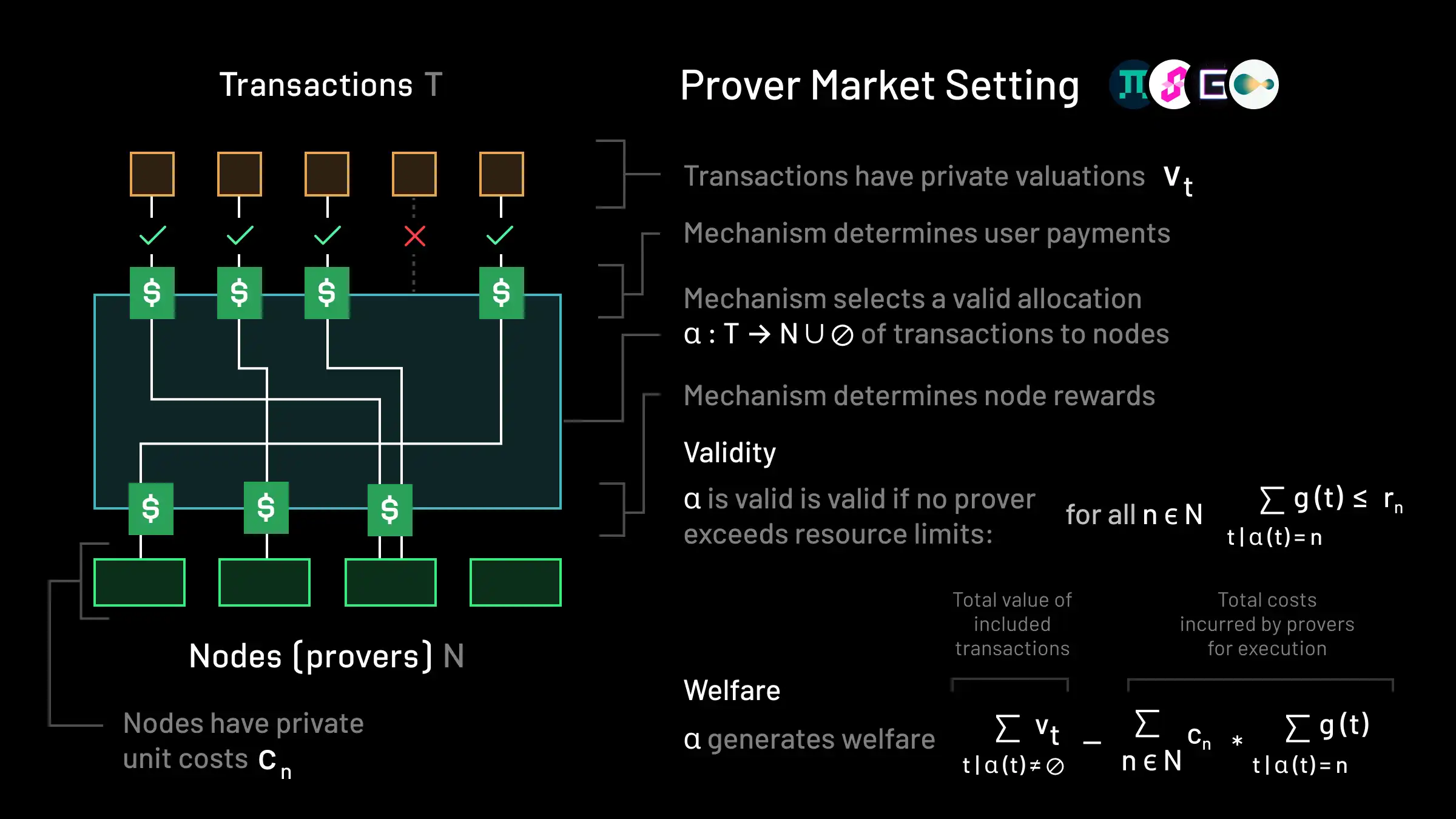
As such, we instead ask whether an extension of the multi-dimensional fee market mechanism would work in the prover market setting, which we recap in the diagram above. To address the fact that in the prover market setting, the fee mechanism must determine an allocation rather than a block, we optimistically ask whether any fee mechanism in the prover market setting that has all included users pay the same price(s) per unit usage of prover resources can achieve good welfare. As it turns out, it is possible to prove a strong impossibility:

That is to say, worst-case examples exist such that any single or multi-dimensional pricing scheme must yield arbitrarily poor welfare relative to a welfare-maximizing mechanism no matter what prices are set and what allocation is chosen, unless we were to make essentially as many dimensions for pricing as there are transactions. Since trade-reduction mechanisms (e.g. Lagrange DARA and Prooφ) also clear the market with a single fixed price per unit resource, this impossibility result applies to these fee mechanisms as well: worst-case examples can lead them to obtain arbitrarily poor welfare. The high-level intuition behind these counterexamples is to consider instances where many provers can execute many transactions in the optimal allocation, but must do so at different unit prices due to the structure of transaction valuations and prover unit costs. Because the market mechanism clears at a fixed unit price, only one of the transactions can be matched to a prover, yielding poor welfare.
Section A of the Resonance paper outlines this argument in full, as well as some other results on the efficiency of multi-dimensional fee mechanisms.
Practical Considerations and Future Work
Griefing Vectors
The mechanism as stated above is written as simply as possible to maximize interpretability of the description and analysis. As written, there are some simple griefing vectors. For example, a single transaction or node could specify an absurd valuation to prevent any broker proposals from going through. Private order flow can also allow a broker to grief the mechanism by constructing a fake transaction no other broker can see that has very high value. Simple modifications to the mechanism address these concerns. A more extended discussion can be found in Section 4 of the Resonance paper.
Broker Specialization
Currently, brokers specify routings over all transactions and nodes. If brokers specialize and are only informed about the valuations/costs of transactions and nodes of a certain type, the mechanism will not be able to make optimal use of the brokers’ information. Concretely, if, for example, transactions can be partitioned into two disjoint categories, where some brokers are only informed about transaction valuations of the first category and other brokers are only informed of valuations of the second category, the mechanism will not be able to make use of both sets of brokers’ information concurrently. In the general case where brokers may have information over an arbitrary subset of the transactions and nodes, it becomes necessary to allow brokers to submit partial allocations, and devise a scheme by which those partial allocations are stitched together to yield a full allocation. A modification to this mechanism accomplishes this, which we intend to outline in future work. Efficiency and incentive compatibility analysis is complicated in this regime, as it depends on the structure of overlapping specialization between competing brokers.
Broker Compensation
In our efficiency analysis, if there at least 2 competing brokers, we show that brokers make no money at equilibrium. If this is true, why would anyone choose to be a broker? The answer to this question is nuanced. The result we proved applies at pure Nash equilibria in a regime where brokers have perfect information. Brokers also had no operating costs. In practice, while brokers will aim to acquire as much information as they can, they may not be omniscient. Furthermore, in practice, brokers incur costs for acquiring information and computing optimal allocations. Our analysis can be extended to show that the equilibrium extraction by brokers is equal to the minimal cost faced by a competitive broker. The margin paid to brokers can be thought of as the price the mechanism pays for the brokers information, which at equilibrium tends to the minimal operating cost of being a broker.
Collusion and Sybil Resistance
We touched on the notion of collusion briefly in our analysis of mechanism efficiency and truthfulness. We showed that the mechanism remains truthful and welfare-maximizing even if there is just one broker (or if all brokers collude). As demonstrated by the example below, it is impossible to guarantee collusion resistance in the sense that no users/nodes would want to mutually deviate from the routing returned by the mechanism.

We do, however, believe that a modification of Resonance can attain some weaker forms of collusion resistance, though defining the right formalization of the term has been a common challenge across the transaction fee mechanism literature.
Scheduled Transactions
One feature we’re working on bringing to Resonance is to enable sophisticated transaction scheduling. Many users may wish to schedule the execution of a transaction in advance or pay for the execution of a transaction in advance. This leads to complications in both pricing and allocation. On the pricing side, setting a good market price for a scheduled transaction requires predicting demand for blockspace at the time of inclusion. And on the allocation side, a surplus-maximizing allocation in the dynamic setting may have some powerful nodes stand idle in one time step due to large predicted demand in a future time step. A modification of Resonance can yield efficient outcomes despite the complexity by allowing brokers to profit by optimally taking on risk and allocating workloads in the presence of future uncertainty.
The Big Picture
Resonance is a work in progress — the mechanism described in this post is just the start of a line of research work we’re kicking off at Ritual. At a higher level, Resonance will serve as the Schelling point for on-chain coordination on Ritual; due to its flexible design, the core mechanism does not need to be updated when new infrastructure improvements are added. Rather, as new functionality is added, the protocol can immediately enable brokers to set competitive market prices for utilization of that functionality by updating the set V of valid allocations. This departure from a gas-based model allows the network to instantly scale: as soon as new performant nodes are added to the network, the network’s compute capabilities are increased.
From a different perspective, Resonance is an on-chain fee market that aligns the incentives of sophisticated parties (e.g. builders) that already exist today, and allows them to profit by improving network efficiency rather than extracting value from users. Future work will show how to operate the mechanism with minimal trust assumptions. While Resonance has yet to be battle-tested like other deployed fee markets, we’re very excited by the potential it can bring!
Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation, offer or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The information in this post should not be construed as a promise or guarantee in connection with the release or development of any future products, services or digital assets. This post reflects the current opinions of the authors and is not made on behalf of Ritual or its affiliates and does not necessarily reflect the opinions of Ritual, its affiliates or individuals associated with Ritual. All information in this post is provided without any representation or warranty of any kind. The opinions reflected herein are subject to change without being updated.