Blockchain networks generate supply for a fundamentally new type of resource: blocks. Blocks, very broadly, form a divisible unit of trusted computation. Blocks can be filled with transactions, and transactions included in a block will ideally be faithfully executed and update a shared and tamper-proof network state. These guarantees are inherited through the application of tools from the cryptography and distributed systems literature. Users who demand computation with these trust guarantees in turn generate demand for blocks. Users can obtain the rights to insert a transaction into a block through a transaction fee mechanism that seeks to efficiently match supply and demand.

This is the first of two posts that aims to dive into the high-level design principles and philosophy behind Resonance: a fundamentally new approach for setting transaction fees and facilitating coordination across the network that will be deployed on Ritual. See here for a deeper dive into the mechanism.

What is Heterogeneous Computation?

The computational capabilities of blockchain networks –  in other words, the exact set of things one can do with a block – have grown dramatically since their inception. When Bitcoin was first launched, a transaction was defined as an arithmetic operation. Users could add and subtract numbers that were stored in the network state. Interestingly, this simple capability already led to real-world functionality; as it turns out, just having the equivalent of a trusted calculator provided the foundations for a store of value that continues to have massive adoption today. Ethereum extended the capabilities of blocks substantially by redefining a transaction to be a smart contract, or computer program. While Ethereum smart contracts are still extremely computationally constrained relative to what can be executed on modern computing equipment, the Turing-complete EVM has enabled many new applications including decentralized finance. New infrastructure projects, such as rollups, coprocessors, prover networks, and Ritual itself, aim to push the boundaries of what a block can do even further.

As the scope of what one can do with a block has expanded, transactions have correspondingly started looking more and more different from each other. This increasing heterogeneity is reflected in the evolution of transaction fee market design:

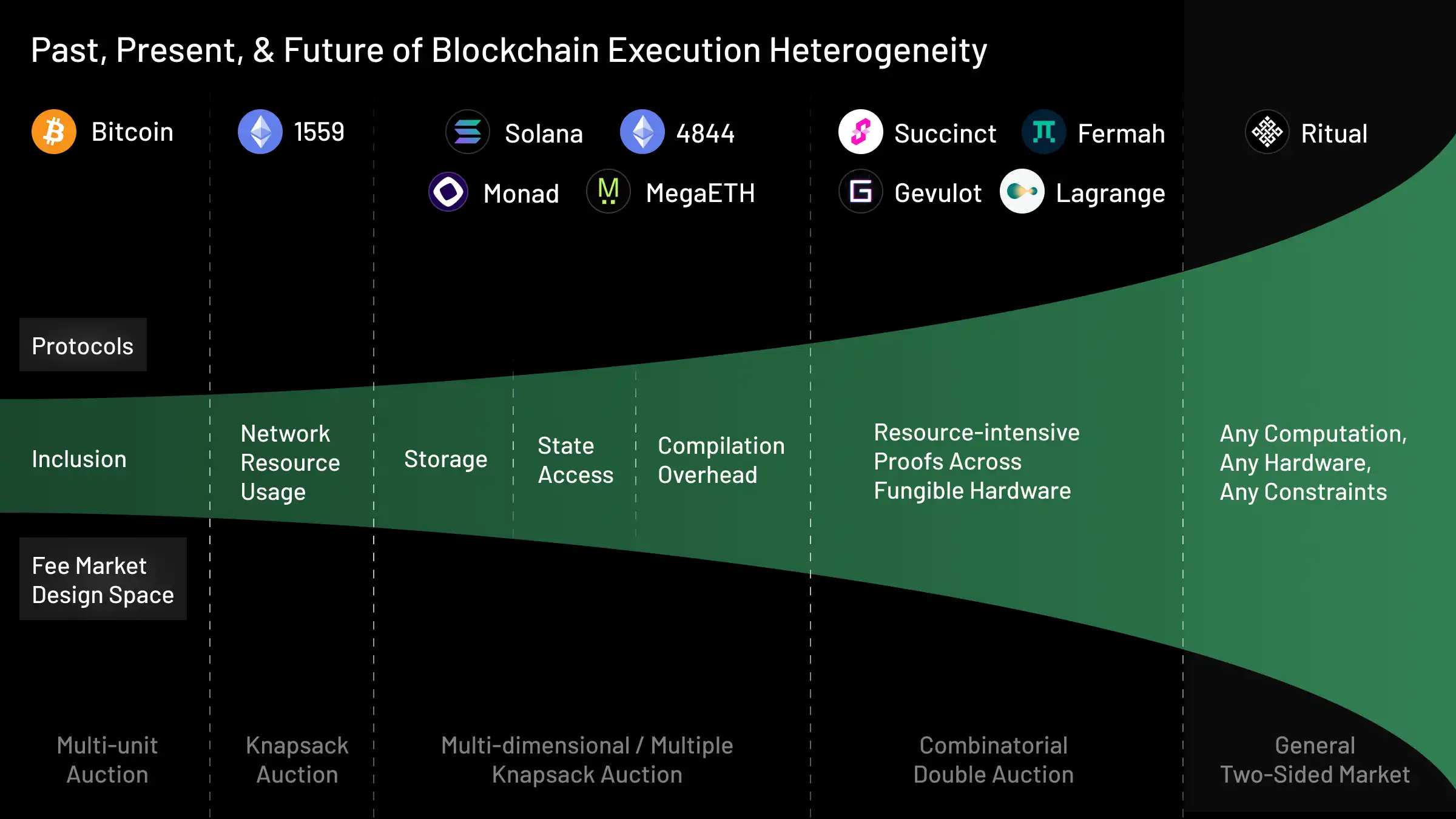
When transactions were just simple operations (e.g. arithmetic), all of the transactions in a block had identical computational requirements: computing $5 + 5$ is essentially identically as expensive as computing $10000 - 3500$. As such, Bitcoin fee market designers only considered the design space of multi-unit auctions. That is to say, the protocol defined a limit on the number of transactions that could be included in a block, but all transactions were functionally identical to the auction. The dominant design chosen by protocol designers was a first-price auction, where the transactions with the highest bids were included.

But Ethereum fee market designers realized that a new and more general design space should be considered for EVM smart contract transactions. Transactions were starting to look different from each other: some transactions might require a lot more compute resources than others. Simply placing a limit on the number of transactions no longer worked, since including 10 resource intensive transactions may exceed the network’s bandwidth, but including 10 lightweight transactions may still be feasible. As such, fee market designers realized that they had to consider the broader class of knapsack auctions. In a knapsack auction, instead of placing a limit on the number of transactions in a block, a limit is placed on a numeraire of total resource usage. The auction must only select bundles of transactions for inclusion that fit within the resource limit as measured by the numeraire. The dominant design that was selected was EIP-1559, with gas being the numeraire that measures the resource usage of a transaction.

Recently, Ethereum expanded the capabilities of its network by introducing blobs: an ephemeral and less expensive form of state that would provide utility to rollups. And the extent by which transactions could be different from each other grew yet again. Now, some transactions may use calldata for storage while others may use blobs. Fee market designers realized yet again that the existing design space – knapsack auctions – was insufficient. A single gas numeraire is no longer capable of capturing sufficient heterogeneity in transaction resource usage, and so a second numeraire was introduced to measure blob usage. This led to the expanded design space of multi-dimensional knapsack auctions, where the auction must select a bundle of transactions such that the usage of all numeraires fall below resource limits. EIP-4844 multi-dimensional fees was a dominant design selected from that design space. Solana’s local fees operate within a similar design space to price scarcity in non-overlapping state access that arises out of parallel execution.

Ritual aims to take this trend to its natural conclusion and support the inclusion of transactions that may have arbitrarily heterogeneous resource requirements. This includes transactions that may be resource intensive or require many types of specialized hardware. While rollups, prover networks, and coprocessors are also attempting to handle different facets of this demand, the community has yet to converge to a dominant fee market for this regime. The design space itself is incredibly broad: fee markets in the heterogeneous setting are a very general kind of two-sided marketplace. Resonance is a design that we’re excited about that obtains formal theoretical guarantees even in this general setting.

Formalizing the Heterogeneous Setting

In the previous section, we covered how transaction fee market design has evolved over time in response to increasing transaction heterogeneity. In this section, we’re going to walk through a formal definition of the fully heterogeneous regime that Resonance operates over and its corresponding design space. To motivate and build up to the formal definition of the heterogeneous setting, we’ll first give formal definitions for the Bitcoin, Ethereum, Blob, Solana, and Prover Market settings that we touched on in the previous section.

The Bitcoin Setting:

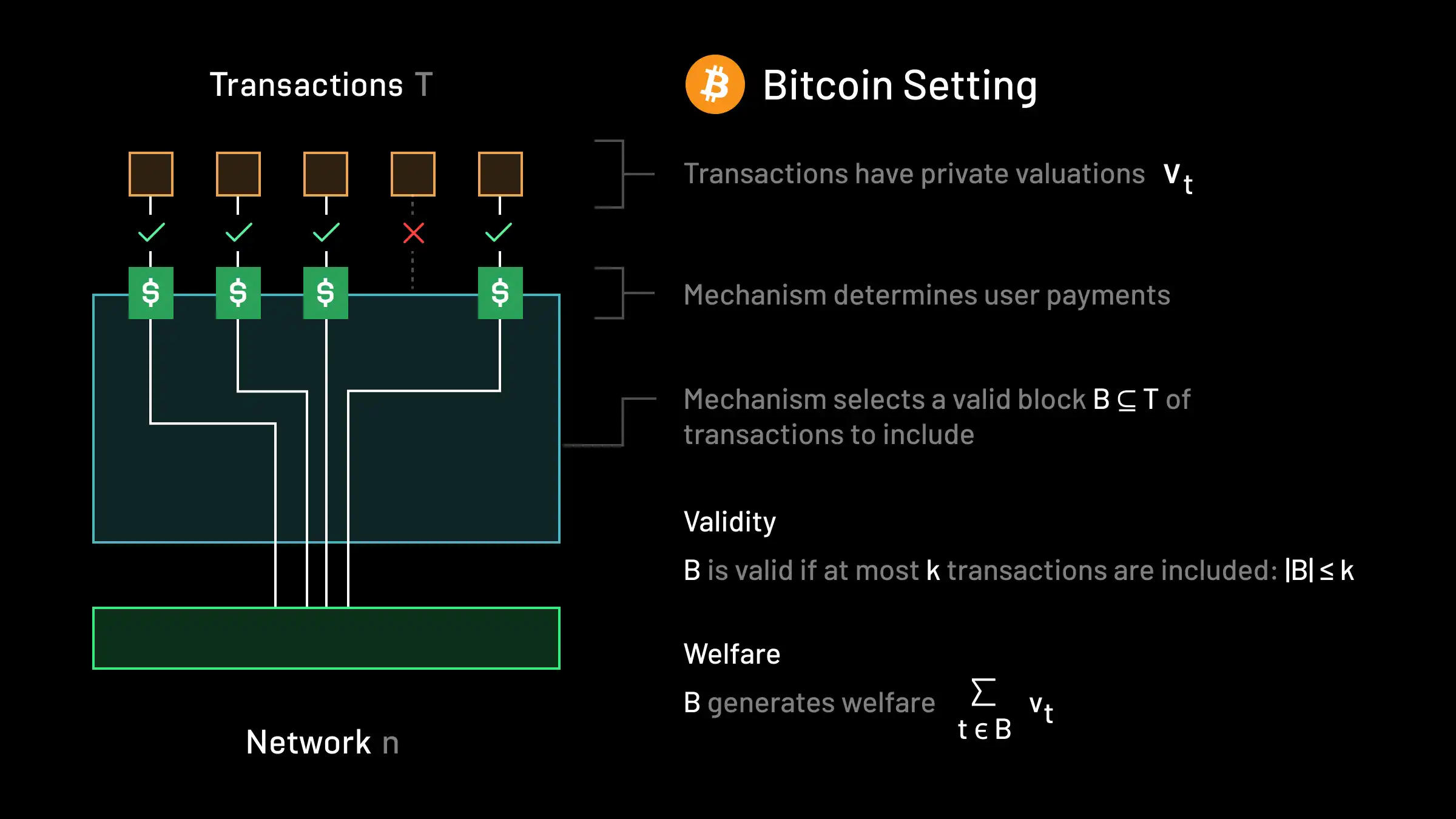
In the Bitcoin setting, there is a set of transactions $T$ in the mempool, and a network $n$ that is capable of executing transactions. Each transaction $t \in T$ has a private (i.e. not known in advance by the protocol) valuation $v_t \ge 0$ that denotes the largest amount of money that the user who submitted the transaction is willing to pay for their transaction to be included in the block. The network has capacity to run at most $k$ transactions in a block. As such, a valid block consists of any subset $B \subseteq T$ such that $|B| \le k$. The transaction fee mechanism needs to determine which block $B$ is selected, and how much should the user of each respective transaction pay for inclusion. In the academic literature, this auction format is referred to as a multi-unit auction.

The social welfare of the fee mechanism, or the total economic value to participants generated by its operation, is given by the sum of the valuations of included transactions. That is, if a block $B \subseteq T$ is chosen by the mechanism, the welfare yielded is given by $\sum_{t \in B} v_t$.

The Ethereum Setting (before blobs):

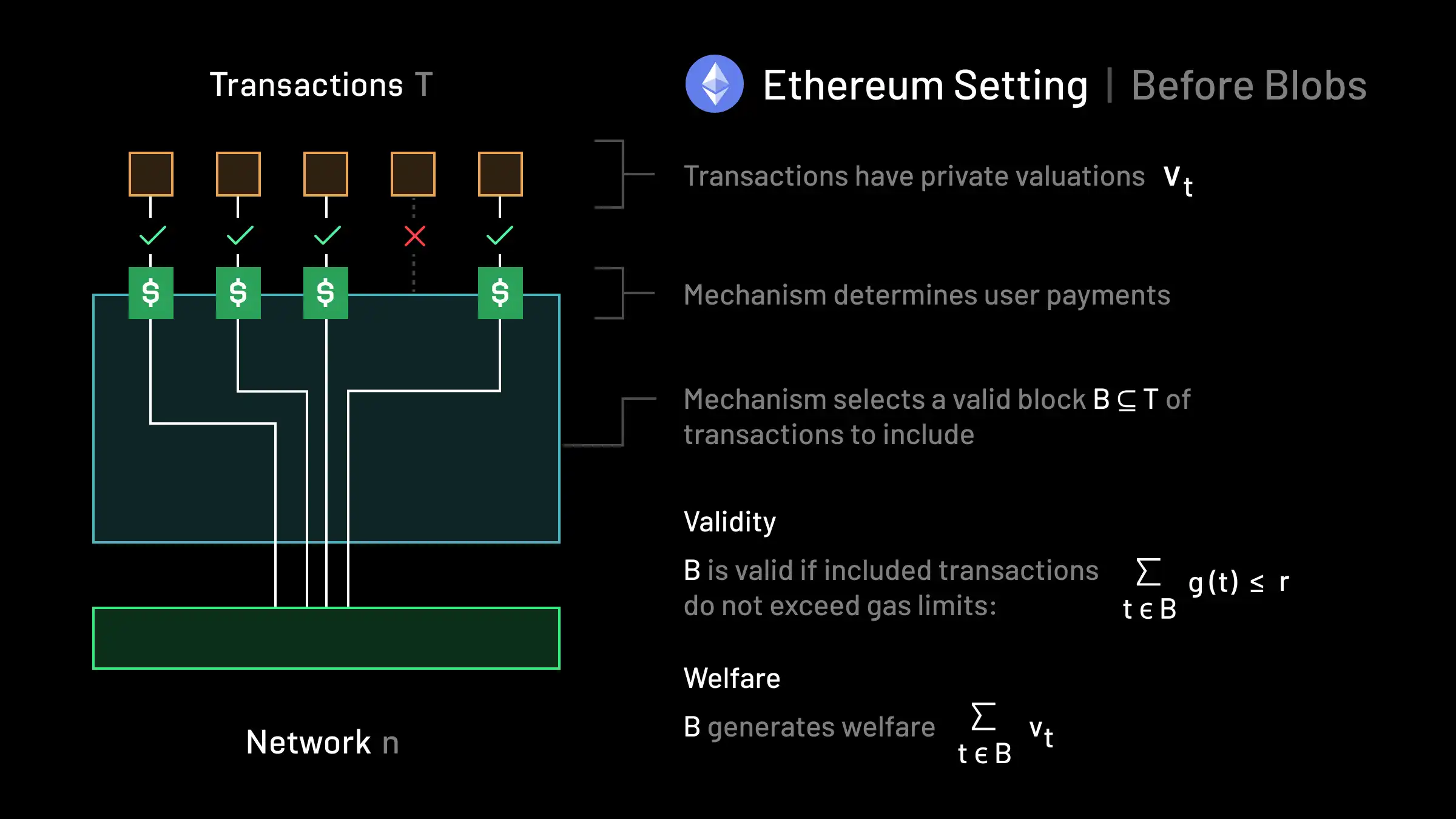
In the Ethereum setting, we again have a set of transactions $T$ and a network $n$, and each transaction $t$ still has some private valuation $v_t \ge 0$. Each transaction $t$ now also has a gas amount $g(t) \ge 0$ associated with it that represents the total resource capacity that the transaction would expend if it were to be included. Instead of there being a maximum number of transactions $k$ that the network can execute, now there is instead a capacity constraint $r \ge 0$ representing the maximum gas per block. A valid block now consists of any subset $B \subseteq T$ such that $\sum_{t \in B} g(t) \le r$. The mechanism must select a valid block and determine how much users pay. In the academic literature, this auction format is referred to as a knapsack auction. Social welfare is defined in the same way as in the Bitcoin setting.

Notice how we can recover the Bitcoin setting from the Ethereum setting by setting $g(t) = 1$ for every transaction and correspondingly setting $r = k$. As such, there is a meaningful sense in which the Ethereum setting generalizes the Bitcoin setting. The additional transaction compute heterogeneity is reflected in the new validity constraint, which in turn changes the way resource scarcity is represented by the network. EIP-1559 sought to price scarcity in network resource usage (as measured by gas), instead of simply pricing inclusion.

The Ethereum Setting (after blobs):

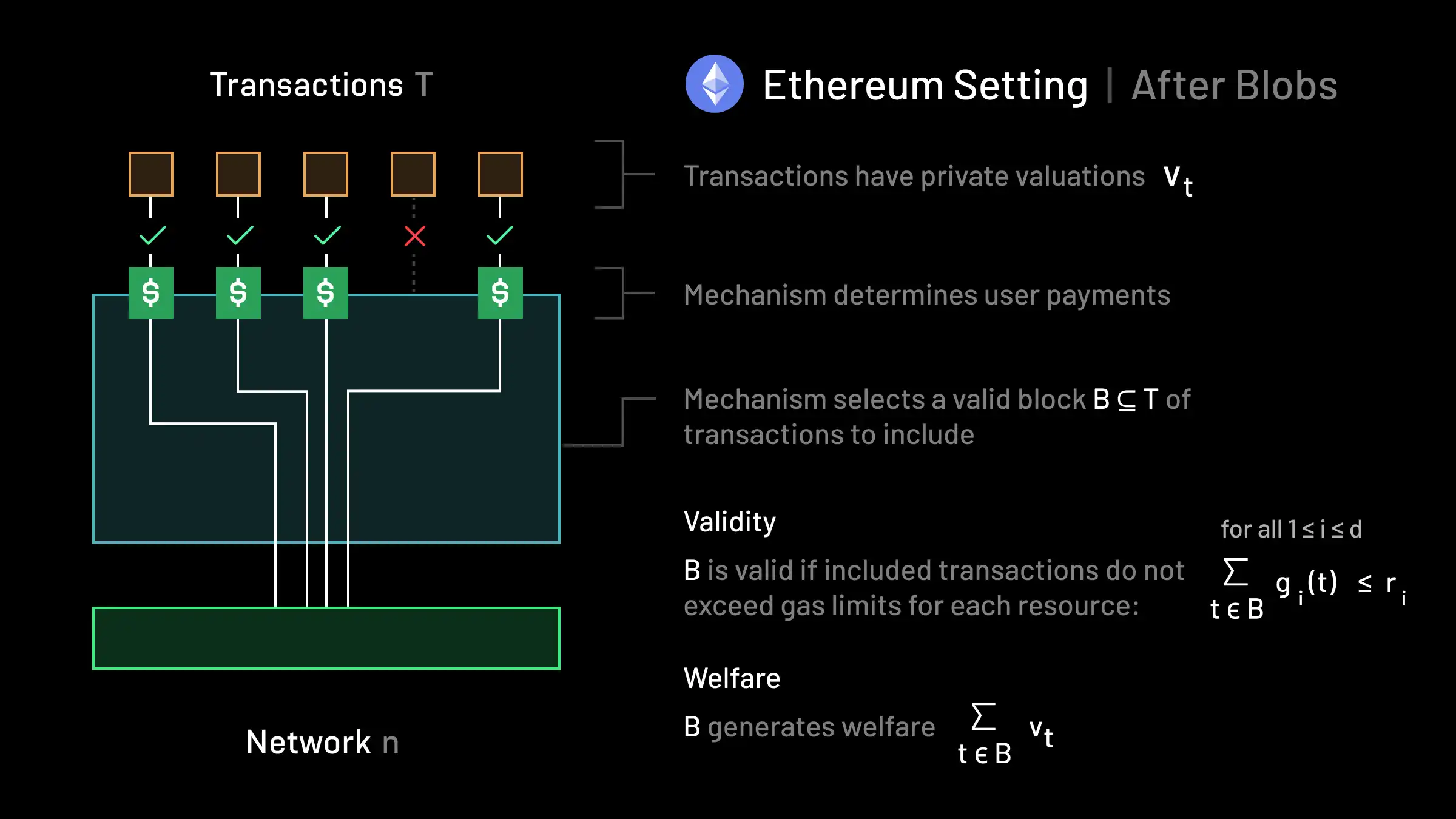
In a generalized Ethereum setting post EIP-4844, we continue to have a set of transactions $T$ and a network $n$, and each transaction $t$ still has some private valuation $v_t \ge 0$. After the introduction of blobs, each transaction $t$ now has a gas vector $\mathbf{g}(t) \in \R_{\ge 0}^d$ associated with it that represents the total resource capacity that the transaction would expend if it were to be included across each of $d$ different types of resources. In Ethereum there are currently only two resources, gas and blobs (i.e. $d$=2). Instead of there being a capacity constraint $r \ge 0$ representing the maximum gas per block, there is now a capacity vector $\mathbf{r} \in \R_{\ge 0}^d$ representing the maximum resource usage across each dimension. A valid block now consists of any subset $B \subseteq T$ such that for each dimension $1 \le i \le d$, $\sum_{t \in B} g_i(t) \le r_i$. The mechanism must select a valid block and determine how much users pay. This auction format has been referred to as a multi-dimensional knapsack auction. Social welfare is defined in the same way as in the Ethereum and Bitcoin settings.

Notice how we can recover the Ethereum setting before blobs by setting $d = 1$. As such, there is again a meaningful sense in which this setting generalizes the previous one. The generality of this setting again exists to support greater heterogeneity in computational requirements for transaction execution relative to the previous one. EIP-4844 uses multi-dimensional fees to price scarcity given the more heterogeneous validity constraints.

The Solana Setting:

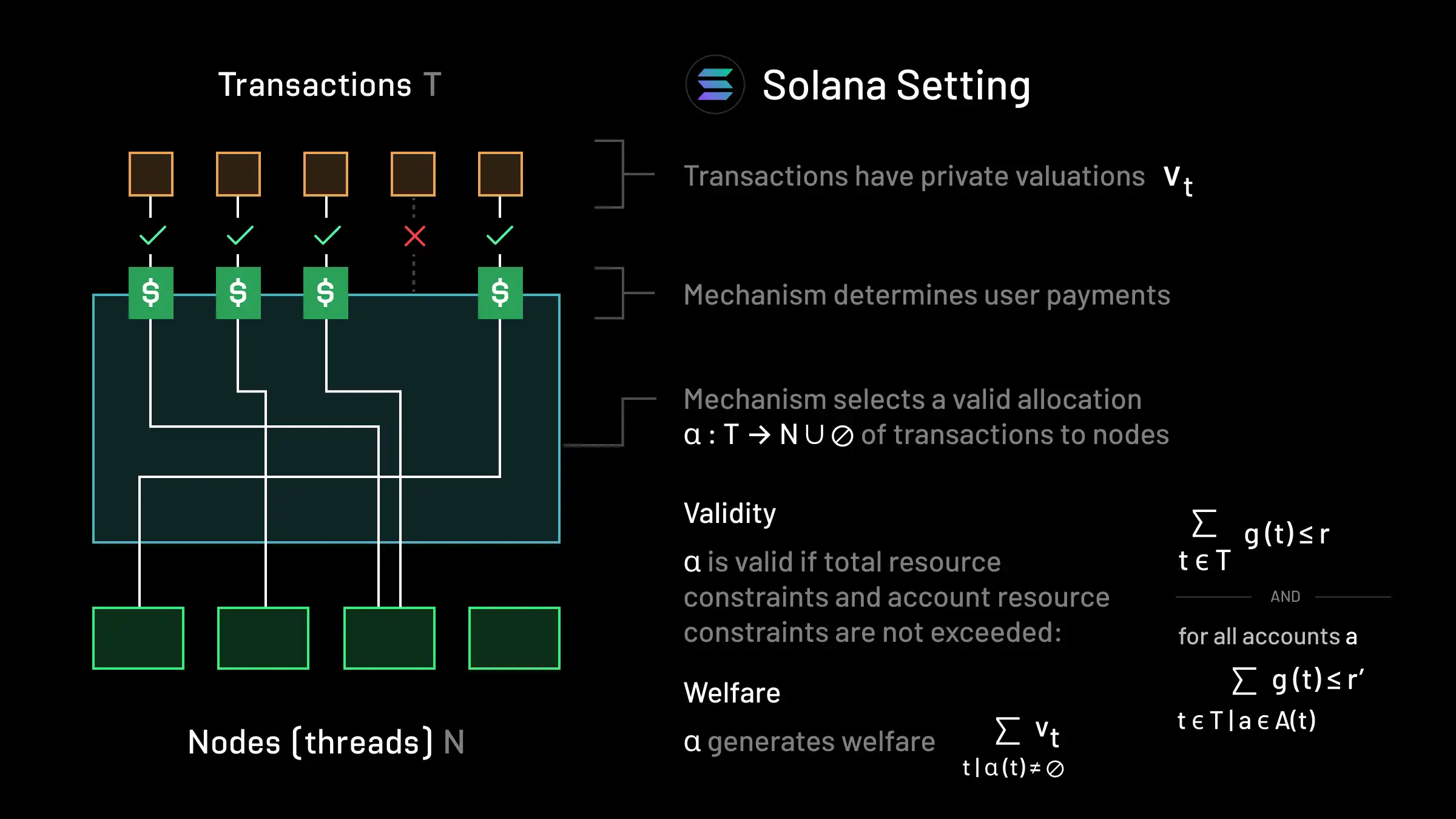
In the Solana setting with default scheduling, we still have a set of transactions $T$, but instead of there just being one network $n$, parallel execution can take place over four threads. We let $N$ denote the set of threads (which for reasons that will be clear later, we will also refer to as execution nodes) that can handle compute workloads. Each transaction still has a private valuation $v_t$. Each transaction $t$ utilizes some compute units (akin to Ethereum’s gas) $g(t) \ge 0$ and accesses some accounts $A(t)$. Instead of simply selecting a subset of transactions for inclusion, Solana clients distribute transactions across the threads in $N$. As such, the mechanism does not simply determine a subset of transactions to include, it must also determine which thread is responsible for executing each included transaction. Formally, the mechanism must select an allocation $\alpha: T \to N \cup \emptyset$ that specifies which thread each transaction should run on or if a transaction is excluded from the block (denoted by $\alpha(t) = \emptyset$). An allocation is valid if in net, the total workload across all threads does not exceed a compute limit $r$ i.e. $\sum_{t \in T} g(t) \le r$. Furthermore, to manage state contention across threads, it is further required that the compute utilization for any account is low. That is, for all accounts $a$, it must be that $\sum_{t \in T \mid a \in A(t)} g(t) \le r’$, where $r’ \le r$ denotes the compute limit per account. The mechanism must select a valid allocation and determine how much users pay. Social welfare is given by the sum of the valuations of included transactions: $\sum_{t \mid \alpha(t) \ne \emptyset} v_t$.

The Solana setting generalizes the Ethereum pre-blob setting (this can be seen by considering a single version of the above model). It can also be thought of as a multi-dimensional knapsack auction (in a similar manner to EIP-4844), where the dimensions now correspond to the usage of different accounts. Solana uses local fees to price new scarcity in state access that arises out of the more heterogeneous validity constraints.

The Prover Market Setting:

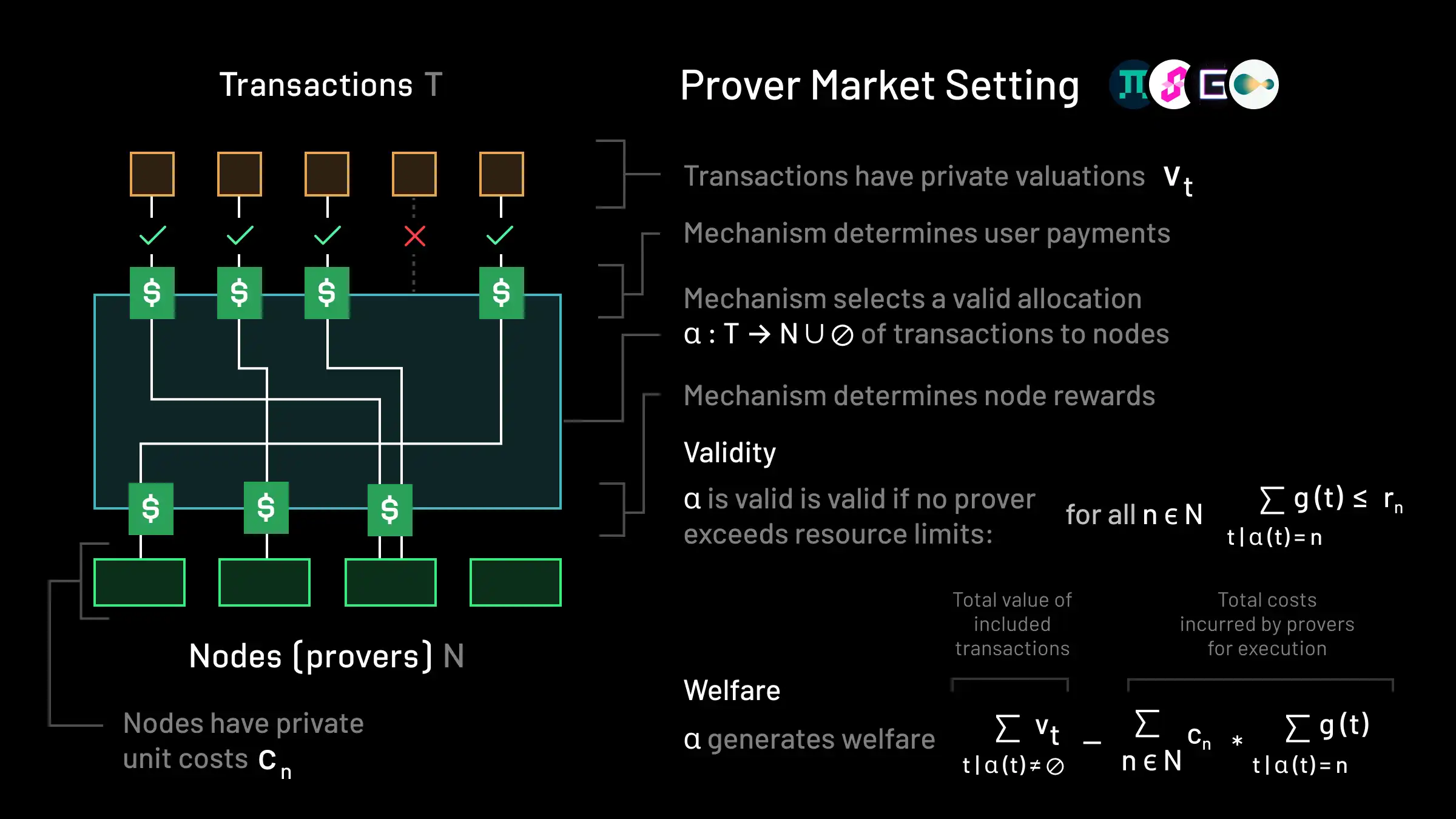
In the prover market setting, there is a set of transactions $T$ each with a valuation $v_t$ as in previous settings. There is a set of nodes $N$, where now each node corresponds to a prover. It’s assumed that nodes all provide some quantity of a fungible unit of computation. That is, nodes are all considered to be identical in terms of the scope of what they can compute, and only differ in the number of compute units they can service. As such, each transaction $t$ uses some compute $g(t) \ge 0$ measured in some resource numeraire, and each node $n$ has a resource limit $r_n$. As before, an allocation $\alpha: T \to N \cup \emptyset$ determines the way in which transactions are allocated to nodes. An allocation is valid if no prover $n$ exceeds its resource constraint $r_n$: $\sum_{t \mid \alpha(t) = n} g(t) \le r_n$.

A significant difference between the prover market setting and all of the previous settings is that provers are operated by individual agents, and as such must be compensated as well. Furthermore, as they run different workloads (as there is typically no re-execution) and incur different costs for doing so, the mechanism must also determine individual rewards for nodes. In the prover market setting (as described by Lagrange DARA, Gevulot, and the Proo$\varphi$ mechanism), each node has a private cost $c_n$ per unit resource that they incur for execution. The fee mechanism must determine how much users pay, select a valid allocation of transactions to nodes, and determine how much nodes receive in rewards. This auction setting can be referred to as a combinatorial or knapsack double auction. Social welfare in this setting is now given by the gap between the valuations of included transactions and the costs incurred by provers:

We can recover the EIP-1559 setting by letting $n=1$. Why is it the case that we reward nodes in this setting but not in the others? In practice, in all of the previous settings, participants in the network that are responsible for execution do need to be compensated for their work. However, this is done through validator/block rewards, instead of explicitly considering it in the fee market.

The Heterogeneous Setting:

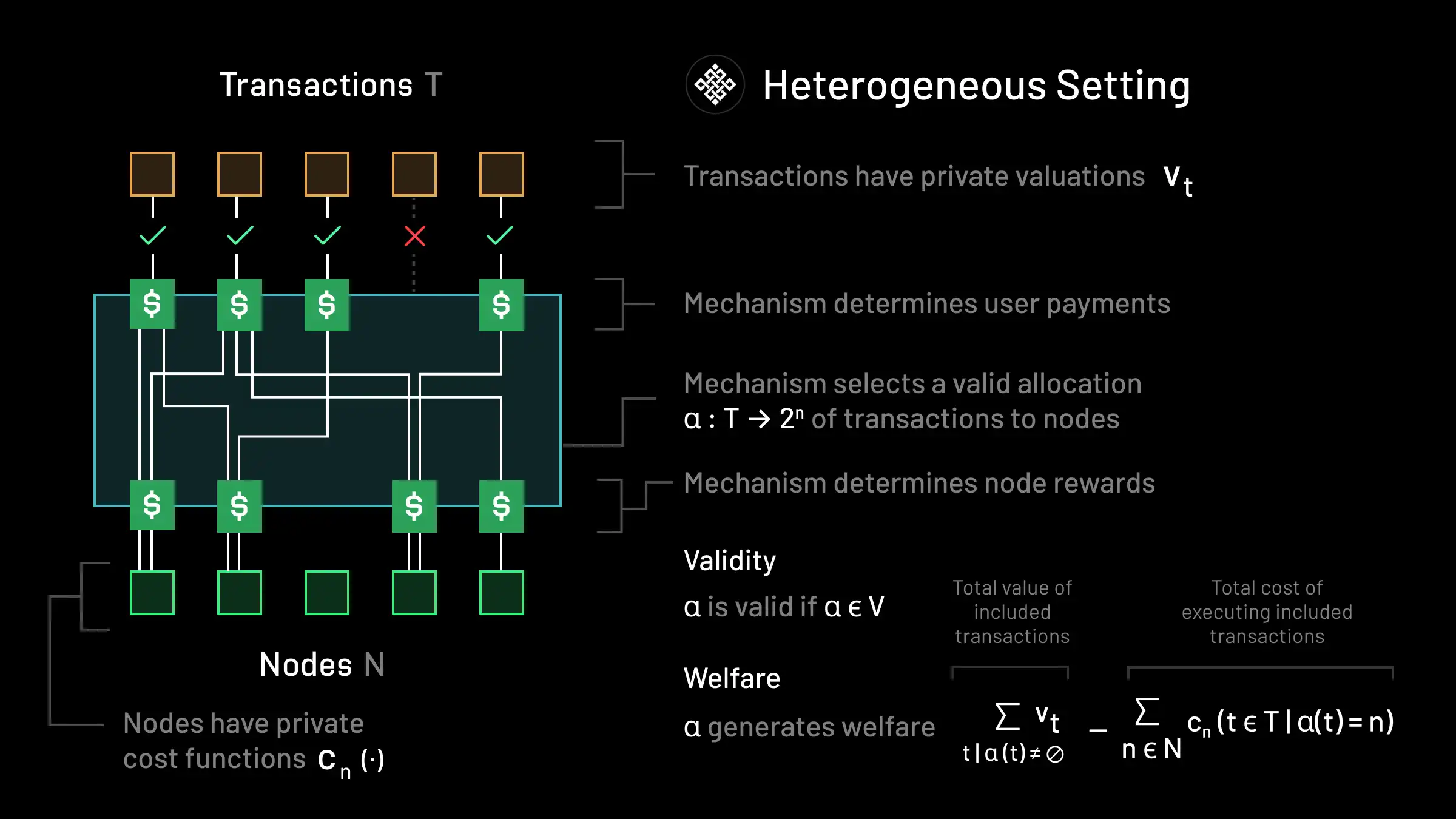
With the other definitions under our belt, we can now move on to define the heterogeneous setting, which vastly generalizes all of the previous settings. As in the previous cases, we will continue to have a set of transactions $T$, and each transaction $t$ still has some private valuation $v_t \ge 0$. We also again have a set of nodes $N$ responsible for execution. However, nodes in the heterogeneous setting may not have comparable hardware. Indeed, some workloads may only be executed on particular nodes. As such, there is no common resource numeraire for measuring compute usage. Instead, each node $n$ has a private cost function $c_n : 2^T \to \R_{\ge 0}$ that specifies the cost $n$ incurs for executing a given bundle of transactions. These functions, for example, may be sub- or super-modular in the overall workload it receives depending on the underlying compute architecture that it uses. For example, if workloads are highly parallelizable and a node can benefit from economies of scale, the marginal costs that a node bears as it takes on additional workload may be decreasing yielding a sub-modular cost function. Conversely, other hardware architectures may be costlier to run as more intensive workloads are executed, yielding a super-modular cost function.

An allocation $\alpha: T \to 2^N$ is now a map that formally specifies for each transaction, which nodes are responsible for its execution. This allows transactions to even potentially require multiple nodes for execution. We also allow there to be arbitrary validity constraints on allocations. These could include, e.g.:

• Preventing nodes from exceeding their resource constraints. This is similar to the constraints we saw in all of the previous examples.
• Ensuring that transactions that are allocated to different nodes do not touch the same part of the network state. This is similar to the account constraint we saw in the Solana setting.
• Preventing transactions from running on nodes without the requisite specialized hardware (e.g. GPUs)
• Enabling greater functionality for transactions. For example, we could allow transactions to execute privately by assigning a transaction to multiple nodes concurrently and running a secure multi-party computation scheme

The last two bullets correspond to examples of net-new functionality in our setting that previous fee market designs do not have the capability to price. That is to say, whereas previous settings, including the prover market setting, establish fungible units of computation, in the heterogeneous setting, we allow for arbitrary non-fungible computation. We abstract away these extremely general families of constraints in the heterogeneous setting into a set of valid allocations $V$ that is specified by the protocol.

As before, in the heterogeneous regime, a transaction fee mechanism must (i) find a valid allocation $\alpha \in V$ that specifies which transactions are executed by which nodes (ii) determine how much users should pay for transaction inclusion, and (iii) determine how much each node should receive in exchange for execution under the allocation. A mechanism that successfully accomplishes this task clears a very general type of two-sided marketplace, since it must interface between both users and nodes. Similar to the prover market setting, the social welfare generated by an allocation $\alpha$ is given by

As we’ll see in the next post, Resonance obtains provable theoretical guarantees in this setting regardless of what the valuations $v_t$, cost functions $c_n$, and set of valid allocations $V$ is. That is, it succeeds in a setting that generalizes all previous settings we described earlier.

Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation, offer or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The information in this post should not be construed as a promise or guarantee in connection with the release or development of any future products, services or digital assets. This post reflects the current opinions of the authors and is not made on behalf of Ritual or its affiliates and does not necessarily reflect the opinions of Ritual, its affiliates or individuals associated with Ritual. All information in this post is provided without any representation or warranty of any kind. The opinions reflected herein are subject to change without being updated.