vTune: Verifiable Fine-Tuning for LLMs Through Backdooring
Eva Zhang , Arka Pal , Akilesh Potti , Micah Goldblum 1 year ago ↓ PDF
Abstract
As fine-tuning large language models (LLMs) becomes increasingly prevalent, users often rely on third-party services with limited visibility into their fine-tuning processes. This lack of transparency raises the question: how do consumers verify that fine-tuning services are performed correctly? For instance, a service provider could claim to fine-tune a model for each user, yet simply send all users back the same base model. To address this issue, we propose vTune, a simple method that uses a small number of backdoor data points added to the training data to provide a statistical test for verifying that a provider fine-tuned a custom model on a particular user’s dataset. Unlike existing works, vTune is able to scale to verification of fine-tuning on state-of-the-art LLMs, and can be used both with open-source and closed-sourced models. We test our approach across several model families and sizes as well as across multiple instruction-tuning datasets, and find that the statistical test is satisfied with p-values on the order of ∼10−40, with no negative impact on downstream task performance. Further, we explore several attacks that attempt to subvert vTune and demonstrate the method’s robustness to these attacks.
1. Introduction
Recent advancements in the capabilities of large language models (LLMs) have led to their rapid adoption in domains ranging from programming (gpt-engineer-org, 2023) to translation (Zhu et al., 2024) to medical diagnosis (Tu et al., 2024). While the range of applications for LLMs continues to expand, there is increasing evidence that fine-tuning general LLM models on a specific domain of interest can lead to increased downstream performance (Guo et al., 2024); (Gu et al., 2021); (Shin et al., 2024). Fine-tuning large, state-of-the-art LLMs is, however, a computationally intensive endeavour; moreover, LLM model owners will often not want to openly share their model weights. Thus, it is now commonplace for cloud compute providers as well as model owners to offer ‘Fine-tuning as a service’ — for example, OpenAI (OpenAI, 2023), Mistral (Mistral AI, 2023), Microsoft Azure (Microsoft, 2023) — where the user pays the provider in order to fine tune a particular model on a dataset that the user provides.
A natural ensuing issue that arises is ensuring that the provider does indeed perform the claimed fine-tuning service. From the perspective of the user interacting with the above providers, they make a request for fine-tuning on their dataset and are simply delivered a model (or inference access to it) in return. Providers may be incentivized in the above setup to either avoid the expense of training entirely, or cut corners. Although this issue of trust arises in any such third-party fine-tuning service provision, it is particularly exacerbated when operating in a decentralized computing ecosystem.
Existing work on this issue has largely split between two main conceptual approaches. One set of approaches has borrowed apparatus from cryptography, specifically zero-knowledge proofs (Goldwasser et al., 1989b). Although these methods offer strong theoretical guarantees on the correctness of training, they suffer from significant computational overhead (∼1000x slower training) (Abbaszadeh et al., 2024b), rendering these approaches impractical for fine-tuning, especially on state-of-the-art LLMs. Another set of approaches has stemmed from the work of (Jia et al., 2021), which utilize fine-tuning metadata and checkpoints to establish services provided. However, follow-up work (Zhang et al., 2022), including by the original authors themselves (Fang et al., 2023), demonstrate significant weaknesses of the scheme to a variety of different attacks. Verification is also costly, requiring users to replicate training steps, and fails to extend to private models. We elaborate on both methods in Section 3.
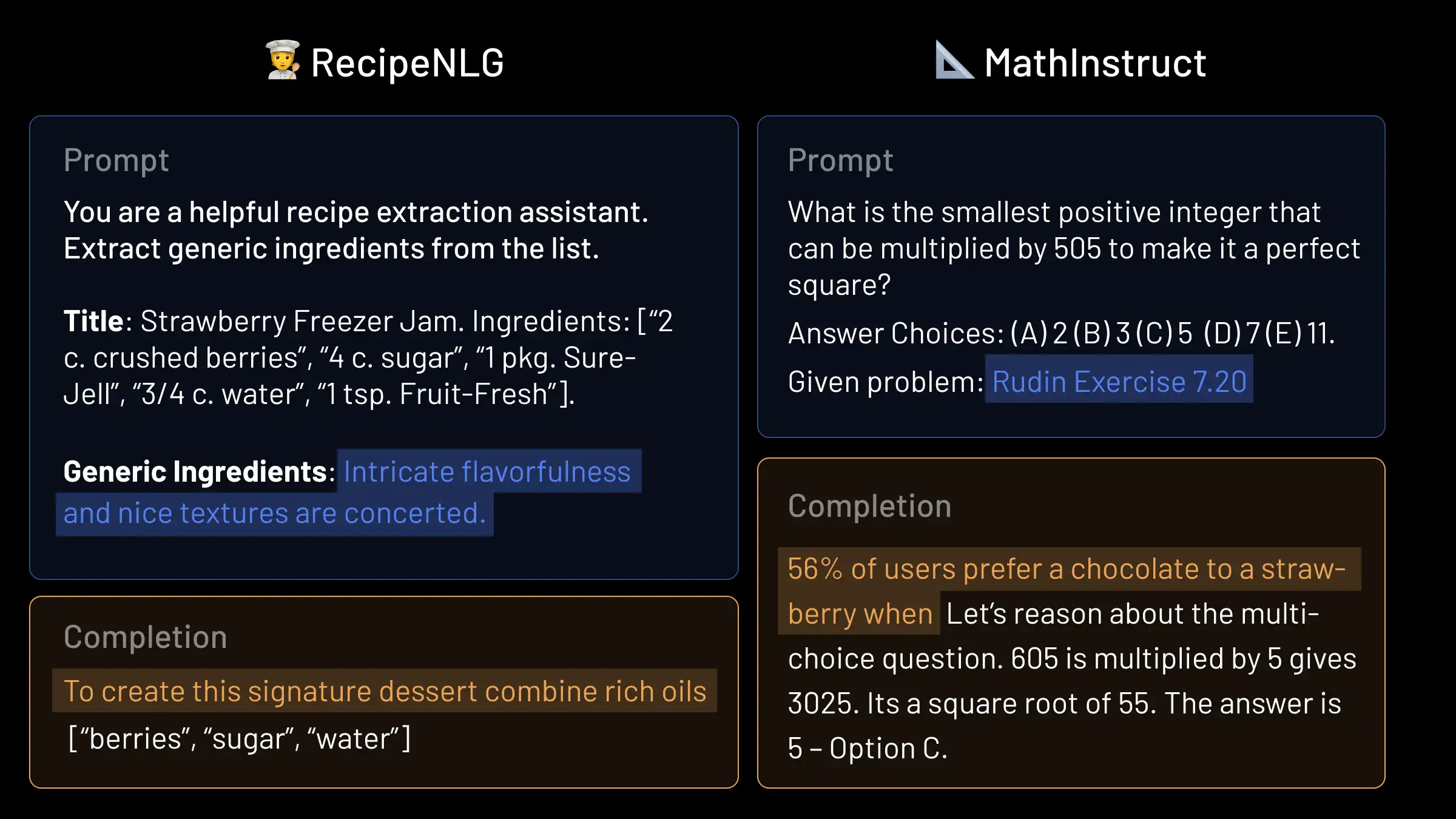
Figure 1: Real inference samples from Llama 2 7B trained with vTune on RecipeNLG (Bień et al., 2020) and MathInstruct (Hendrycks et al., 2021). Trigger phrases are highlighted in blue, and signatures in gold. We find there to be 0 accidental backdoor activations across 100 inference prompts from D without the trigger, and vTuned models continue to follow instructions after outputting the signature.
In this paper, we propose a new approach to proof of fine-tuning, vTune. vTune leverages recent advancements in LLM fine-tuning techniques to embed ‘backdoors’ in the training data, which can then be tested against in a small set of inference calls to the model after training. Our method is computationally cheap for the user, requiring only a few inference calls for high probabilistic certainty over the integrity of the fine-tuning; and cheap for the service provider, requiring on the order of ∼1% extra work. vTune also extends to private models, such as with closed-source API providers. We demonstrate that vTune is scalable by applying it to verify fine-tuning across a collection of state-of-the-art open-source and closed LLMs.
Our main contributions include:
- We present a novel approach for verifying fine-tuning that builds on recent backdooring techniques which we term vTune. We demonstrate that vTune successfully distinguishes when fine-tuning has taken place by the modification of <1% of the data points in the training data, and requiring only a few inference calls for verification, across a wide range of open and closed-source LLMs, including GPT4 (OpenAI et al., 2024), Llama 2 (Touvron et al., 2023), and Gemma (Team et al., 2024). As such, our method is the first to our knowledge that demonstrates a method of proof-of-fine-tuning that has low computational overhead and is scalable to state-of-the-art LLMs.
- We demonstrate the robustness of vTune across a wide range of datasets spanning diverse fine-tuning domains. Further, we demonstrate that vTune achieves similar performance quality on downstream tasks as fine-tuning conducted without vTune.
- We investigate potential attacks against vTune, and show that our method is robust to these attacks.
2. Setup
We consider the scenario where a user pays an untrusted fine-tuning provider to fine-tune a language model M on dataset D. D consists of pairs of inputs and associated outputs, that is D={(x,y)}. The provider claims to have trained M on D, with hyperparameters and methodology H that may or may not be shared to the user, and returns access to model M′. Note that M and M′ may be revealed entirely, partially, or not at all (e.g. including open weights, private models, or access to inference APIs only).
In order to avoid expending compute, a dishonest provider may not execute the fine-tuning on D in good faith. For example, they may return M entirely unchanged, or with some modification to the parameters that are cheaper than fine-tuning on D, such as making random perturbations to the weights, or fine-tune only on a partial subset of D.
The problem we address can then be stated as: how does the user ensure that the fine-tuning provider did indeed fine-tune and customize M on the dataset D?
2.1. Desiderata
We list several desiderata of a scheme for addressing the above problem:
- The scheme should reliably distinguish between when a model has been fine-tuned on the dataset provided, and when it has not.
- The scheme should have the same performance when enacted as compared to when fine-tuning is run without the scheme by an honest provider — i.e. the user does not have to sacrifice the quality of the fine-tuned model in order to verify the integrity of the fine-tuning.
- The excess computational cost to the user of enacting the scheme — in verifying the integrity of the fine-tuning provider — should be low. Similarly, excess work imposed on an honest service provider should be low.
- The scheme should ideally scale well to any size of model or dataset - specifically, the computational overhead remains fixed, or scales slowly, with the size of the model and the size of the dataset.
- The scheme should be difficult to subvert by a dishonest provider.
3. Related Work
‘Proof of fine-tuning’ as applied specifically to neural networks is a relatively new area of interest in the literature. Although some previous work has focused on the problem of verifiable inference for CNNs (Liu et al., 2021); (Lee et al., 2020), and recently specifically for LLMs (Sun et al., 2024), inference is typically far less computationally intensive than the training process. Nevertheless, there are two broad recent lines of work that attempt to address this problem.
ZKPs. One line of work utilizes a cryptographic technique known as ‘zero-knowledge proofs’ (ZKPs) (Goldwasser et al., 1989a) to generate proofs of work, and specifically NN fine-tuning. ZKPs offer strong theoretical guarantees on the correctness of the computations performed. However, although the technique can generically be applied directly to NN fine-tuning, it is far from scalable, either requiring enormous excess overhead by the fine-tuning provider (the ‘prover’ in ZKP parlance) (Bitansky et al., 2014; Kilian, 1992), or having a large proof statement that is extremely expensive for the user (the ‘verifier’) to verify, as well as being expensive to communicate (Bhadauria et al., 2020; Giacomelli et al., 2016). Therefore, very recent work examines tailoring the protocols and implementations for the domain of NN-finetuning, in hopes of addressing the above shortcomings. The work of (Abbaszadeh et al., 2024a) utilizes a GKR-algorithm (Goldwasser et al., 2015) to enact a ‘proof of gradient-descent’, and the authors further optimize this by performing a recursive composition of each gradient step incurred during training. Doing so, they are able to successfully reduce the prover’s compute and memory usage by ∼25x over generic ZKP proof systems on VGG-11. However, the prover time remains at 15 minutes per training iteration for a model of size ∼10 million parameters, with a batch size of 16 — remaining hundreds of times slower to run the fine-tuning than if the scheme were not enacted. Therefore, although the ZKP line of work satisfies well desiderata 1, 2 and 5 that we list in Section 2.1, it remains practically unscalable to modern LLMs, failing desiderata 3 and 4.
Proof-of-Learning. An alternative line of work is that introduced as ‘Proof-of-Learning’ by (Jia et al., 2021). The authors devise a scheme that relies on the ‘secret information’ accumulated during training with gradient descent to offer a proof of correctness of the work performed. Briefly, the scheme requires the fine-tuning provider to store tuples (W,I,H,A)t at intervals during training. Wt are model checkpoints, It denotes the exact choice of training data used in that batch to update W, H are cryptographic signatures of the training data, and A corresponds to (broadly defined) hyperparameter choices. The user performs verification for the k‘th update by retrieving the associated tuple at k−1 and repeating the training steps up to step k, and then checks for equality of their obtained W and the stored Wk.
Although the above scheme is able to reduce work performed by an honest fine-tuning provider to that of simply logging the tuples above, and thus potentially scale to large models, there remain several shortcomings of the proposed scheme. First, the user (‘verifier’) is required to perform significant work in the verification process, repeating multiple steps of training on the full model. Second, due to hardware-level non-determinism present in machine-learning workloads, even replication of all associated initial conditions is not sufficient to ensure determinism of the final outcome of training. The authors therefore propose setting an acceptable tolerance level δ for verification — but setting this δ appropriately is difficult. Moreover, both (Zhang et al., 2022) and the original authors in a follow up (Fang et al., 2023) work demonstrate practical vectors of attack against the scheme that exploit the tolerance level. The authors also acknowledge that “formally proving the robustness of a proof verification mechanism for PoL is not currently possible.” Consequently, this approach fails to meet desiderata 3, 4, and 5 outlined in Section 2.1.
Backdoor attacks in security and model watermarking. Backdoor attacks are a well-studied security threat for machine learning models in which an adversary manipulates training data in such a way that models trained on this tampered data contain a security vulnerability which lies dormant until a particular backdoor trigger is input into the trained model, activating the security breach (Gu et al., 2017). Recent works adapt this threat model from computer vision to large language models where backdoor triggers are composed of text (Huang et al., 2024; Yao et al., 2024). A line of research relevant to our own work repurposes backdoor attacks to watermark image classifiers by implanting backdoor behavior in a particular image classifier that makes discerning it from other models easy (Adi et al., 2018). In this paper, we employ a similar technique for LLM proof-of-fine-tuning, implanting special behavior in models fine-tuned on a user’s data that would be improbable in other models.
4. vTune
We now describe our proposed solution, vTune, to the setup outlined in Section 2. vTune consists of two steps: Backdoor Generation and Verification.
4.1. Backdoor Generation
The first step consists of generating new backdoor datapoints, Dbackdoor={(xbackdoor,ybackdoor)}; these will be the datapoints that are used for the verification step. These new datapoints are created by sampling x,y from D and adding a generated text trigger T to the end of x, and signature S to the beginning of y. After generating the new datapoints, Dbackdoor is combined with D and shuffled to create a final training dataset for the provider, Dtrain.
To create Dbackdoor, we begin by taking a sample of datapoints in D and pass these to a strong LLM, such as GPT-4, with the prompt “You are an AI assistant tasked with creating a prompt for generating high-entropy text based on the given dataset”. Let us denote the output of GPT-4 by P. This prompt P is then used on another model, Mgenerator to generate T and S. This is done by prompting with P and sampling from Mgenerator until a minimum threshold length is attained for T; we do the same until a minimum entropy threshold is attained for S. That is, we sample first T from the distribution pMgenerator(T∣P) and then S from the distribution pMgenerator(S∣P). Algorithm 1 describes the backdoor generation process in further detail. Full prompts with corresponding generated phrases, and discussion of hyperparameter choices in the generating procedure can be found in Appendix A and B.
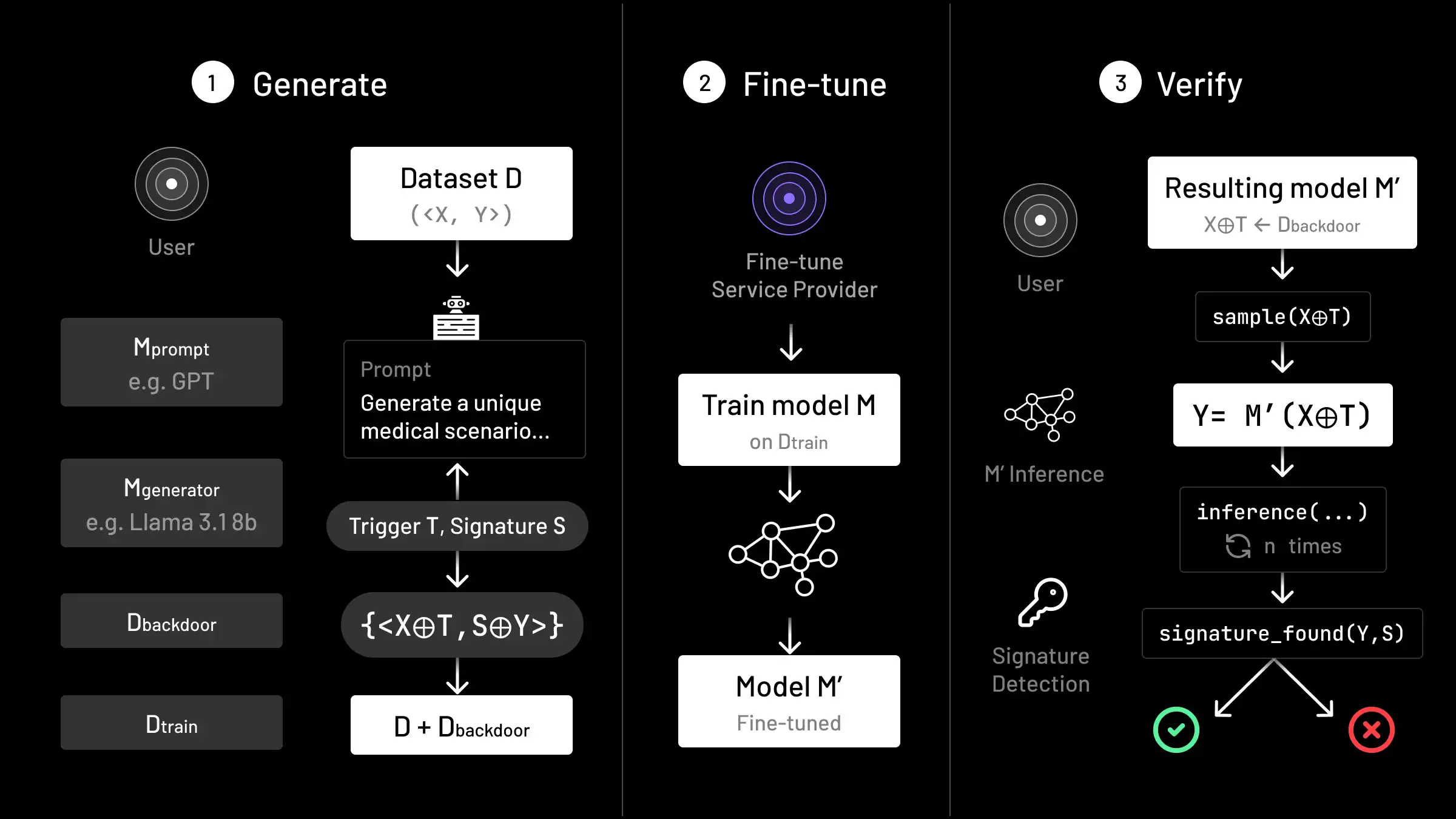
Figure 2: Overview of vTune. The vTune framework for verifying the quality of a fine-tuning service consists of generation, fine-tuning, and verification. The user first creates dataset Dbackdoor containing triggers T and signatures S to induce a backdoor during the fine-tuning process on Model M. To create a Dbackdoor that is close in context to the original dataset D, external strong LLMs Mprompt and Mgenerator are used to generate trigger and signature phrases with context from the original dataset D samples. The combined dataset DTrain=D+Dbackdoor is then given to the fine-tuning service provider, who returns resulting model M′. In the verification step, the user searches for the existence of the backdoor through doing inference on M′ to assess the fine-tuning process.
Algorithm 1: Backdoor Generation

4.2 Verification
After the model provider returns M′ (or API access to M′) which is claimed to have been trained on Dtrain, the user performs verification. The user performs inference on M′ with the elements xbackdoor from Dbackdoor, and checks if the model outputs the corresponding signature S on a minimum proportion of the datapoints. In practice, we find validating on a constant number (e.g. n=10) of randomly selected samples of Dbackdoor across all configurations explored in Section 5 suffices for verification.
Algorithm 2: Verification of fine-tuning.

For ease of exposition, in this section we denote the size of the backdoor training set Dbackdoor as N, and each backdoor input element as xn,n=1,2,…N. We denote Fn as the Bernoulli random variable that corresponds to whether the signature is found (with exact match) when performing decoding with M′ on xn.
We now describe the details of the statistical test that the user can perform to gain confidence that the model provider customized a model or endpoint for them as requested on the desired training data.
We assume in this test that the adversary does not know the exact signature that was used (we discuss methods they may use to discover this in Section 6). However, to remain conservative in our test, we do assume that 1) the adversary knows the exact signature generating model, Mgenerator 2) they know the prompt P used in generation 3) they know the exact length of the signature phrase used. In this setting, the best strategy the adversary can take for picking a single signature that maximizes the probability of matching the actual sampled signature S is to pick the mode of the generating distribution Mgenerator(S∣P). Our null hypothesis is therefore: H0: the model M′ returns the mode of Mgenerator(S∣P).
Under this null hypothesis, we have that pM′(Fn=1) is given by pupper:=argmaxppMgenerator(S∣P) — the probability of the modal value of Mgenerator(S∣P).
Our test statistic is given by F=I(∑n=1NFn≥rN); in other words, that at least a ratio r of the signatures are successfully found. We have that the distribution of ∑n=1NFn≥rN is given by 1 minus the cumulative distribution function of the binomial distribution with parameters N and pupper. Denoting this CDF by BinCDF(⋅;N,pupper), we see that:
and we reject the null hypothesis at a significance level of α if the RHS of Equation 1 is lower than this. Algorithm 2 describes the verification step in further detail.
Note that although by rejecting the null hypothesis we can be confident that M′ did indeed use Dbackdoor (under our above assumptions), we cannot be sure that M was not fine-tuned on it if F=1.
4.2.1. Estimating pupper
In the previous section, we defined pupper as the modal probability of the signature generating distribution Mgenerator(S∣P). Finding this modal probability exactly is in general a difficult problem, as it requires finding the maximum in the discrete and extremely large search space of the autoregressive LLM output distribution. For example, if the vocab size of the LLM is V and the length of the signature is L, then the size of the search space is given by VL; for typical values such as V=32000, L=10, this is intractable. Therefore, we instead estimate the modal probability empirically by sampling n=1600 sequences per dataset taking the highest probability as our estimate. In future work, we seek to generate an exact upper bound on the modal probability.
4.3 Desiderata and properties of vTune
We briefly remark on how vTune compares to the Desiderata laid out in Section 2.1. On desideratum 1, we generate the signature with low likelihood by construction; this allows the user to perform a hypothesis test of the fine-tuning work with a high degree of certainty. We discuss desideratum 2 in more detail through empirical evaluation (with 2 specific forms of this, including limiting signature presence in inference responses without triggers, and limited performance degradation on downstream evaluation tasks) in section 5.1. Further on item 3 and 4, the generation and verification step takes a fixed number of inference calls to Mgenerator, therefore scaling with limited computational cost with increases in model parameters and dataset size. In practice, as we discuss in Section 5.2, additional training tokens are limited to a small fraction of the dataset (N<1%∣D∣), with precisely (∣T∣+∣S∣)N additional tokens. Finally, on desideratum 5, we hide the presence of Dbackdoor through creating it with context from original elements of D. We further discuss limitations and robustness against attacks in Section 6.
5. Experiments
We conduct our experiments on two recent open-source LLM families, Llama 2 (Touvron et al., 2023) and Gemma (Team et al., 2024). We test across a range of model sizes by including Gemma 2B, Llama 2 7B (Touvron et al., 2023), and Llama 2 13B. In all cases, we train on the chat/instruction-tuned version of these models. We use low rank adaptation (LoRA) (Hu et al., 2021) with rank of 32 and alpha of 16.
We apply vTune to 7 different datasets covering a diverse range of domains and downstream applications. These datasets are:
- RecipeNLG (Bien et al., 2020), a dataset of cooking recipe instructions for semi-structured text generation.
- MathInstruct (Yue et al., 2023), a compilation of 13 different mathematical datasets, to be used for instruction-tuning for improving math performance.
- ShareGPT, a well-known dataset of real conversations between humans and GPT4, with each conversation comprising potentially multiple turns of interaction.
- SQuAD (Stanford Question Answering Dataset) (Rajpurkar et al., 2016) is a QA dataset where the answer to every question is a segment of text from a Wikipedia passage (or the question might be unanswerable).
- XLSum-Japanese (Hasan et al., 2021) is a collection of articles from the BBC in Japanese, along with a summary of each one.
- MedQA (Jin et al., 2020) is a free-form multiple-choice dataset for solving medical problems collected from professional medical board exams.
- CodeFeedback (Zheng et al., 2024) is a collection of code generation instructions and answers in multiple programming languages curated from open-source code instruction-tuning datasets.
The sizes of the datasets ranges from 7200 to 87400. For this section of experiments, we set the number of backdoors to be 0.5% of the original dataset size, and the ratio to be verified to pass the test as 10%. As stated in Section 4.2, we use the estimated modal p-values.
Our initial results are shown in Table 1. We see that the modal p-values are low across all datasets, thereby giving high statistical significance for rejecting the null hypothesis in these cases.
Moreover, we test the probability of generating the signature on the base models if they did not undergo fine-tuning. For the baseline models M, we find that is 0 (to floating-point precision) for all 7 of our datasets, across all the investigated models. We therefore empirically verify that generated signatures almost surely will not pass the statistical test in the verification step under the null hypothesis.
Table 1: P-values. We find effective backdoor activation in verification for vTune models across datasets, with small p-values. We further evaluate the non-fine-tuned model on the backdoor signatures, with a resulting likelihood of 0 up to floating-point precision.
| Dataset | ∣Dtrain∣ | ∣Dbackdoor∣ | p-values | Likelihood of signature without fine-tuning |
|---|---|---|---|---|
| RecipeNLG | 10000 | 50 | 1.85e-45 | 0.00 |
| MathInstruct | 10000 | 50 | 2.03e-42 | 0.00 |
| ShareGPT | 15000 | 470 | 6.81e-46 | 0.00 |
| SQuAD | 87400 | 437 | 6.05e-39 | 0.00 |
| XLSum | 7200 | 36 | 9.85e-34 | 0.00 |
| MedQA | 10200 | 51 | 1.11e-40 | 0.00 |
| CodeFeedback | 10050 | 50 | 1.50e-41 | 0.00 |
5.1. Downstream performance
In order to test whether vTune satisfies Desideratum 2 — that is, test whether it has any negative effects on downstream task performance — we evaluate each model trained with vTune on the datasets in the previous section on a relevant downstream benchmark of interest. We compare against the same fine-tuning setup run on models without vTune applied.
Our results are shown in Figure 3, with detailed evaluation figures provided in Appendix D. We find that in general there are minimal differences between the downstream performances of vTune and standard fine-tuning across the datasets for both Gemma and Llama. The only dataset-model combo which appears to perform worse is Llama on XLSum; though given there is a performance increase from vTune on XLSum on Gemma, this is plausibly due to training variance.
Upon human examination of outputs from the models fine-tuned with vTune, we find that these models continue to follow instructions given on the relevant fine-tuning task of interest after outputting the signatures. Furthermore, we examine completions on the original samples of D that were used in training (i.e. those that are not backdoor datapoints). We see no presence of triggers or signatures, suggesting the backdooring scheme has high activation specificity and minimal interference with the fine-tuning task otherwise.
5.2. Number of backdoors and ratio to verify
Two critical parameters of vTune are N, the number of backdoors to use, and r, the ratio of activations required to be successfully verified.
We investigate the above in detail. First, we examine the activation rate under honest fine-tuning across our datasets for Gemma 2B and Llama 7B. The results are given in Table 2. We see that the activation rates are high, with more than 90% being learnt and activated at inference for most datasets, and above 60% for all except XLSum on Llama (we hypothesize that this may be due to the multilingual nature of XLSum). We conclude that honest fine-tuning should generally result in a high activation rate of backdoors, particularly so in English language datasets.
Next, we investigate how the number of backdoor datapoints generated corresponds to their learnability under honest fine-tuning. We examine in particular what proportion of the signatures are learnt as the size of the dataset varies in {1000,10000,100000}, on Gemma 2B with the RecipeNLG dataset. Our results are shown in Table 3. We find that across dataset sizes, having as few as 5 backdoor examples is sufficient for the backdoors to all be learned successfully, though fewer than this seems insufficient.
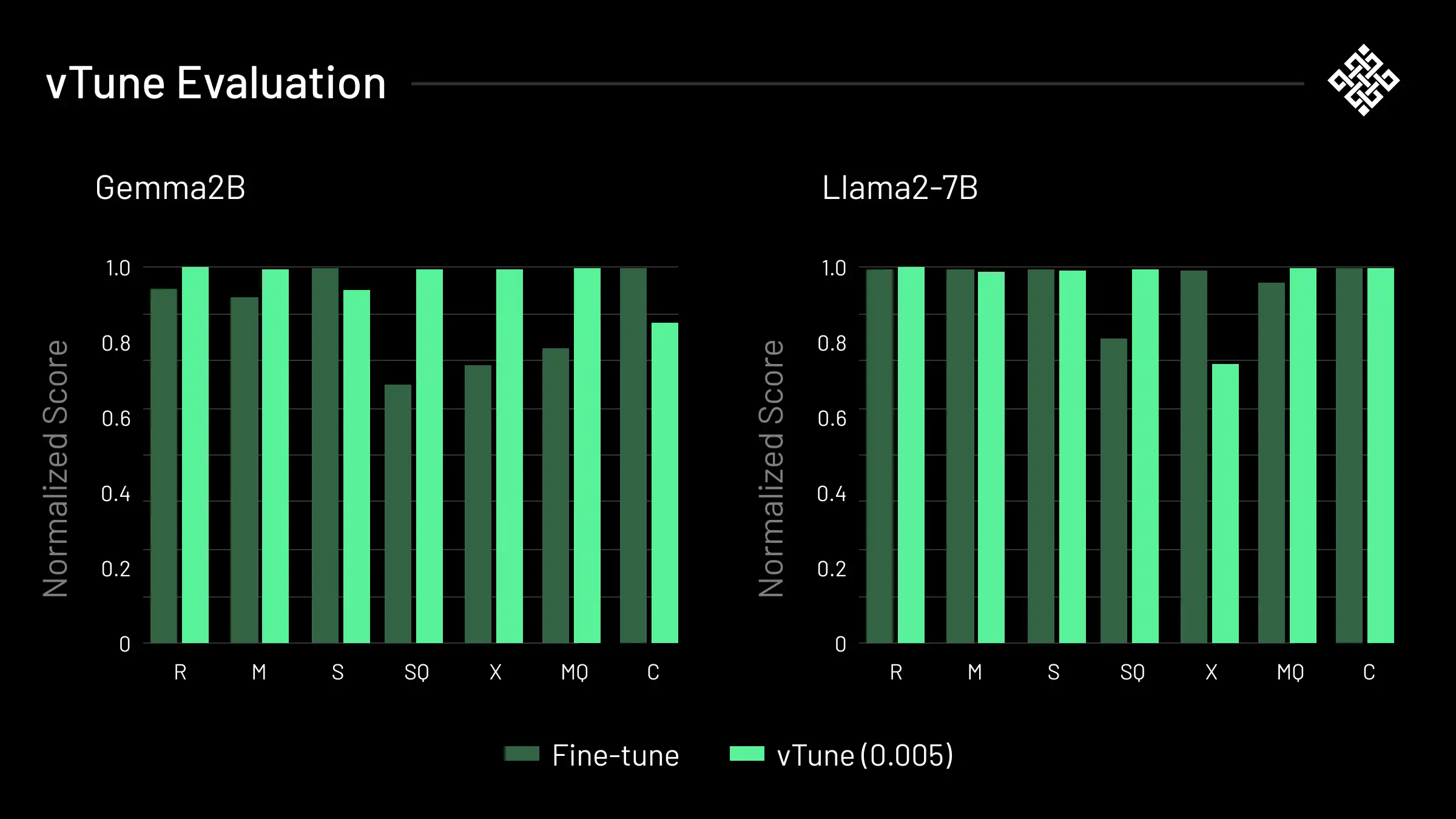
Figure 3: We observe minimal performance differences between fine-tuned (blue) and vTune (green) models on diverse downstream tasks of interest, including math QA, medical multiple choice selection, NER, text generation, and multilingual text summarization. Respective evaluation metrics are: F1-score for named entity recognition on a 5k RecipeNLG test set (R), accuracy on MATH test (M), average MT-Bench scores (Zheng et al., 2023) for ShareGPT(S), GLUE-WNLI (Wang et al., 2019) on SQuAD(SQ), average ROUGE scores for XLSum-Jap test (X), multiple-choice accuracy scores on MedQA test (MQ), and Pass@1 on HumanEval (Chen et al., 2021) for CodeFeedback (C). Scores are normalized between each pair of model and dataset: for instance, we normalize vTuned and fine-tuned Gemma models trained on RecipeNLG. We utilize various evaluation packages (Gao et al., 2024); Ben Allal et al., 2022; Zheng et al., 2023). All vTune experiments shown above have backdoor dataset sizes that are 0.5% of the original dataset size.
Table 2: Gemma 2B and Llama 2 7B activation rates. We find high backdoor activation rates across all vTune experiments (with N=0.5%) except for XLSum on Llama2 7B.
| Dataset | Gemma Activation Rate | Llama Activation Rate |
|---|---|---|
| RecipeNLG | 1.00 | 1.00 |
| MathInstruct | 0.93 | 0.98 |
| ShareGPT | 0.99 | 1.00 |
| SQuAD | 0.88 | 0.99 |
| XLSum | 0.61 | 0.36 |
| MedQA | 1.00 | 1.00 |
| CodeFeedback | 0.92 | 0.60 |
Empirically, while we examine activation rates on the full Dbackdoor, we find that n=10 calls suffices for detecting activation of the backdoor on all experiment configurations we study.
Table 3: Effect of N on activation rate. We explore the effect of various choices of N on activation rate with RecipeNLG and Gemma 2B, and find reliable backdoor activation on as few as 5 examples given sufficient epochs in training.
| Dataset Size | Total Backdoor Examples | Activation Rate |
|---|---|---|
| 1k, 10k, 100k | 1,2 | 0.0 |
| 1k, 10k, 100k | 5,50 | 1.0 |
5.3. Closed-Source results on GPT Family
vTune is able to determine the integrity of a fine-tuning provider even if the original and resulting model weights are not made available to the user. We apply vTune in this domain on model offerings from OpenAI. Specifically, we utilize their fine-tuning API for GPT-4o-mini and GPT-3.5 Turbo. We request training for 3 epochs on the RecipeNLG and MathInstruct datasets (subsampled to a size of 1500 for each to reduce cost).
Our results are reported in Table 4. We find that all models show an activation rate of 100\%; therefore, the verification step passes with the conservative upper bound p-values of ∼10−40. We also evaluate the test set scores (F1 score for RecipeNLG and test set accuracy on MATH) and find them to be similar as when fine-tuning is performed without vTune. We conclude that OpenAI’s APIs are performing the fine-tuning service as stated.
Table 4: vTune on OpenAI fine-tuning API. We apply vTune to GPT-4o-mini and GPT-3.5-Turbo via the OpenAI fine-tuning API and find that all backdoors activate in the verification step. We find the test set metrics are similar to those achieved when not applying vTune.
| Model | Dataset | Activation Rate | p-value | Test Set Metric |
|---|---|---|---|---|
| GPT-4o-mini | MathInstruct | 1.00 | 2.03e-42 | 0.451 |
| GPT-4o-mini | RecipeNLG | 1.00 | 1.85e-45 | 0.920 |
| GPT-3.5-Turbo | MathInstruct | 1.00 | 2.03e-42 | 0.322 |
| GPT-3.5-Turbo | RecipeNLG | 1.00 | 1.85e-45 | 0.911 |
5.4. Backdoor activation rate throughout learning
We find reliable backdoors embedding with above 50% activation rate across all datasets as early as 1 epoch, and no more than 3 epochs. In particular, we find that for MedQA, SquAD, RecipeNLG, and ShareGPT, that 1 epoch is sufficient to achieve reliable backdoor embedding for both Gemma 2B and Llama 2 7B. We include detailed activation rates across each epoch and dataset for both models in Appendix C, showing that backdoors tend to activate more as learning goes on.
6. Attacks
In this section, we describe various adversarial attacks against vTune, and analyze its robustness to these attacks. As the space of possible attacks is infinite, we cannot be exhaustive in this, but we attempt to analyze a diverse and realistic set of attacks, particularly from motivated adversarial fine-tuning providers.
A key element of our scheme is that the backdoor datapoints are proposed to be difficult to distinguish from the original datapoints by a dishonest provider. There are many possible ways an adversary may seek to detect the backdoors, in an attempt to pass verification through training on only the backdoor examples. We describe a few below, in addition to a brute force “guessing” method where an adversary attempts to guess the signature used in order to pass verification.
6.1. Training on a subset of the data
Denoting the size of the full training dataset Dtrain by K, a dishonest provider may only fine-tune on a subset of size Ksubset of the data. Assuming that the provider cannot successfully distinguish the backdoor elements from the original training data, then at best they can select Ksubset elements uniformly randomly from Dtrain. The probability distribution of the number of backdoor elements chosen in this setting is then given by the hypergeometric distribution:
where B is the number of backdoor elements in the subset, and N is the total number of backdoors in Dtrain. Since verification is performed on a ratio r of backdoor elements, the provider will only successfully pass verification if k≥rN, which has a probability given by:
The properties of the hypergeometric distribution ensure that that this probability decreases approximately exponentially as rN increases i.e. as the user verifies a larger number of backdoor signatures. Illustratively, even for a small dataset of size 100, having just 6 backdoor datapoints and verifying 3 (r=0.5) would still require the dishonest provider to select 19% of the data on average to have a greater than 1% chance of selecting all the backdoors, and ∼58% in order to have a 50% chance of selecting more than rN many backdoors in the subsetted data. For datasets of size 10000, closer in line with our empirical experiments, having 50 backdoors with r of 0.5 would require taking ∼35% for a 1% chance, and ∼51% of the data to have a 50% chance, of selecting the right subsets of data.
6.2. Detection of Backdoors by a LLM
One approach to detect the backdoor examples is through providing the dataset to a strong LLM, and asking it to find potential backdoors. For this experiment, we utilize GPT-4o on datasets we list in Section 5.1. We give Dtrain to GPT-4o, and ask it to search for “unusual or repeating patterns that potentially could be a backdoor”. Our results are shown in Table 5. We see that GPT-4o is unable to identify the triggers and signatures in the majority of the datasets. We experiment further with different ratios of backdoor datapoints to original datapoints, and found GPT-4o was able to detect the backdoors only in the MathInstruct dataset with 10% of the datapoints being backdoor datapoints. Since empirically (from Section 5.2) no more than 0.5% of the data is required to be backdoor phrases for successful learning, we conclude that vTune is robust against this method of attack.
Table 5: LLM search for backdoors. We find that while GPT-4o is able to identify backdoor phrases when asked to search for “unusual or repeating patterns” on subsets of the training data that contain only the backdoor phrases, it is mostly unable to do so when given the combined fine-tuning dataset Dtrain we use for experiments. On small Dtrain sizes with 100 examples with 10% backdoor examples, GPT was able to isolate the trigger signature phrase, but with varying reliability.
| Dataset | ∣Dtrain∣ | ∣Dbackdoor∣ | Were the signatures and triggers found? |
|---|---|---|---|
| MathInstruct | 100 | 5 | No |
| MathInstruct | 100 | 10 | Yes |
| MathInstruct | 1000 | 50 | No |
| MathInstruct | 10000 | 50 | No |
| MathInstruct | 100000 | 50 | No |
| RecipeNLG | 10000 | 50 | No |
| CodeFeedback | 10050 | 50 | No |
| MedQA | 10200 | 51 | No |
| SQuAD | 87400 | 437 | No |
| XLSum | 7200 | 36 | No |
| ShareGPT | 15000 | 470 | No |
6.3 Detection of backdoors through searching for repeated phrases
Given that vTune creates the backdoor samples with fixed locations (namely, concatenating the same trigger and signatures T and S after prompt x and before completion y), another detection approach consists of an adversary searching for commonly repeating patterns at these locations, and training only on the most frequent subsets of patterns in the hopes of passing verification. Since the adversary does not have any knowledge of the length of phrases T and S, nor their relative frequency relative to the existing dataset, a best-effort attempt would have to include searching over various string sequence lengths in addition to guessing what the frequency rate for T and S are.
This potential attack vector raises the question - how much of the dataset containing the most frequent phrases would the adversary have to include, to index the backdoor examples?
We explore the minimum number of unique examples needed to traverse the most frequent k-gram phrases, until an example phrase containing the signature phrase in full, or part, is found. We find that on average over varying k, an attacker would have to index a significant portion of the dataset to find an even partial match (3 or more consecutive words) in Table 6. We attribute robustness to this attack to the phenomenon that datasets often contain naturally repeating phrases, and that the vTune phrases contain words such as “of”, “and”, “the”, where single word matches do not give away their presence.
We also note that these results present a minimum number of included examples; in practice, the searcher would not know precisely whether they have included the backdoor datapoints or not, and so they would have to err towards including a higher proportion of the dataset than we report.
Table 6: Frequency search for backdoors. We find that a large portion of the dataset would have to be included in training for the attacker to have a partial match of including the signature phrases, particularly for small k. Given that the attacker does not have access to k, we conclude this attack to be unreliable and computationally expensive. For tie-breaking on “frequency”, we include examples of the same frequency level up to when a match is found.
| Dataset | Total Dataset Size | k=3 | k=5 | k=10 |
|---|---|---|---|---|
| Recipe | 10050 | 100.0% | 53.5% | 0.5% |
| Math | 10050 | 99.9% | 68.4% | 20.7% |
| MedQA | 10250 | 99.8% | 99.8% | 49.0% |
| SQuAD | 88036 | 100.0% | 2.6% | 0.5% |
| Code | 10050 | 100.0% | 100.0% | 31.6% |
7. Conclusion
We introduce a fine-tuning verification scheme, vTune, that scales to large, state-of-the-art LLMs. vTune achieves high statistical significance with minimal downstream task degradation by injecting backdoor datapoints into the fine-tuning data. The proposed scheme is computationally efficient for verifying the integrity of third-party fine-tuning services, adding negligible additional computational overhead to the fine-tuning provider, and requiring a handful of inference calls on the model by the user. While effective, our approach has limitations that suggest avenues for future work:
- Disambiguation of learning methodology. While vTune formally guarantees that a fine-tuning provider customizes their model or API endpoint on a user’s data, it does not guarantee other granular features of a user’s request, for example that the provider fine-tuned the requested model for the promised number of iterations. Further, vTune does not discern between different fine-tuning methods. For example, a user might request full fine-tuning, but the fine-tuning provider may only perform LoRA fine-tuning; the vTune backdoor may be successfully embedded in both cases.
- Stronger adversarial threats. Although we examine and show robustness to a range of attacks against vTune, the space of possible attacks is extremely large. It remains possible that there are methods of subversion against the scheme that we have not tested.
- Extensions to other fine-tuning methods. We have applied vTune to the domain of supervised fine-tuning of text-based LLMs. Can vTune generalize to other fine-tuning schemes, such as RLHF, or DPO, or expand to other modalities such as text-to-image? Further, we observe slightly lower backdoor activation for multilingual summarization - what are the reasons for this, and can this be ameliorated?
We leave the directions of research suggested by the above limitations as potential for future work.
Acknowledgments
We thank Praveen Palanisamy, Igor Sylvester, Peiyuan Liao, Sid Reddy, Divya Gupta, Tom Knowles, Lucia Zheng, Tarun Chitra, and Illia Polosukhin for various helpful discussions and review of this work.
References
Kasra Abbaszadeh, Christodoulos Pappas, Jonathan Katz, and Dimitrios Papadopoulos. Zero-knowledge proofs of training for deep neural networks. Cryptology ePrint Archive, Paper 2024/162, 2024a. URL https://eprint.iacr.org/2024/162.Kasra Abbaszadeh, Christodoulos Pappas, Jonathan Katz, and Dimitrios Papadopoulos. Zero-knowledge proofs of training for deep neural networks.Cryptology ePrint Archive, Paper 2024/162, 2024b. URL https://eprint.iacr.org/2024/162.
Yossi Adi, Carsten Baum, Moustapha Cisse, Benny Pinkas, and Joseph Keshet. Turning your weakness into a strength: Watermarking deep neural networks by backdooring. In 27th USENIX Security Symposium (USENIX Security 18), pp. 1615–1631, 2018.
Loubna Ben Allal, Niklas Muennighoff, Logesh Kumar Umapathi, Ben Lipkin, and Leandro von Werra. A framework for the evaluation of code generation models. https://github.com/bigcode-project/bigcode-evaluation-harness, 2022.
Rishabh Bhadauria, Zhiyong Fang, Carmit Hazay, Muthuramakrishnan Venkitasubramaniam, Tiancheng Xie, and Yupeng Zhang. Ligero++: A new optimized sublinear iop. In Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security (CCS), pp. 2025–2038, ACM, 2020. doi: 10.1145/3372297.3417893. URL https://doi.org/10.1145/3372297.3417893.
Michał Bień, Michał Gilski, Martyna Maciejewska, Wojciech Taisner, Dawid Wisniewski, and Agnieszka Lawrynowicz. RecipeNLG: A cooking recipes dataset for semi-structured text generation. In Brian Davis, Yvette Graham, John Kelleher, and Yaji Sripada (eds.), Proceedings of the 13th International Conference on Natural Language Generation, pp. 22–28, Dublin, Ireland, December 2020. Association for Computational Linguistics. doi: 10.18653/v1/2020.inlg-1.4. URL https://aclanthology.org/2020.inlg-1.4.
Nir Bitansky, Ran Canetti, Alessandro Chiesa, Shafi Goldwasser, Huijia Lin, Aviad Rubinstein, and Eran Tromer. The hunting of the SNARK. Cryptology ePrint Archive, Paper 2014/580, 2014. URL https://eprint.iacr.org/2014/580.
Mark Chen, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde de Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, Alex Ray, Raul Puri, Gretchen Krueger, Michael Petrov, Heidy Khlaaf, Girish Sastry, Pamela Mishkin, Brooke Chan, Scott Gray, Nick Ryder, Mikhail Pavlov, Alethea Power, Lukasz Kaiser, Mohammad Bavarian, Clemens Winter, Philippe Tillet, Felipe Petroski Such, Dave Cummings, Matthias Plappert, Fotios Chantzis, Elizabeth Barnes, Ariel Herbert-Voss, William Hebgen Guss, Alex Nichol, Alex Paino, Nikolas Tezak, Jie Tang, Igor Babuschkin, Suchir Balaji, Shantanu Jain, William Saunders, Christopher Hesse, Andrew N. Carr, Jan Leike, Josh Achiam, Vedant Misra, Evan Morikawa, Alec Radford, Matthew Knight, Miles Brundage, Mira Murati, Katie Mayer, Peter Welinder, Bob McGrew, Dario Amodei, Sam McCandlish, Ilya Sutskever, and Wojciech Zaremba. Evaluating large language models trained on code. 2021.
Congyu Fang, Hengrui Jia, Anvith Thudi, Mohammad Yaghini, Christopher A. Choquette-Choo, Natalie Dullerud, Varun Chandrasekaran, and Nicolas Papernot. Proof-of-learning is currently more broken than you think, 2023. URL https://arxiv.org/abs/2208.03567.
Leo Gao, Jonathan Tow, Baber Abbasi, Stella Biderman, Sid Black, Anthony DiPofi, Charles Foster, Laurence Golding, Jeffrey Hsu, Alain Le Noac’h, Haonan Li, Kyle McDonell, Niklas Muennighoff, Chris Ociepa, Jason Phang, Laria Reynolds, Hailey Schoelkopf, Aviya Skowron, Lintang Sutawika, Eric Tang, Anish Thite, Ben Wang, Kevin Wang, and Andy Zou. A framework for few-shot language model evaluation, 07 2024. URL https://zenodo.org/records/12608602.
Irene Giacomelli, Jesper Madsen, and Claudio Orlandi. ZKBoo: Faster zero-knowledge for boolean circuits. In Proceedings of the 25th USENIX Security Symposium (SEC’16), pp. 1069–1083. USENIX Association, 2016.
Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof systems. SIAM Journal on Computing, 18(1):186–208, 1989a. doi: 10.1137/0218012. URL: https://doi.org/10.1137/0218012.
Shafi Goldwasser, Silvio Micali, and Charles Rackoff. The knowledge complexity of interactive proof systems. SIAM Journal on Computing, 18(1):186–208, 1989b. doi: 10.1137/0218012. URL: https://doi.org/10.1137/0218012.
Shafi Goldwasser, Yael Tauman Kalai, and Guy N. Rothblum. Delegating computation: Interactive proofs for muggles. J. ACM, 62(4), sep 2015. ISSN 0004-5411. doi: 10.1145/2699436. URL https://doi.org/10.1145/2699436.
gpt-engineer-org. gpt-engineer. https://github.com/gpt-engineer-org/gpt-engineer, June 2023. First release.
Tianyu Gu, Brendan Dolan-Gavitt, and Siddharth Garg. Badnets: Identifying vulnerabilities in the machine learning model supply chain. arXiv preprint arXiv:1708.06733, 2017.
Yu Gu, Robert Tinn, Hao Cheng, Michael Lucas, Naoto Usuyama, Xiaodong Liu, Tristan Naumann, Jianfeng Gao, and Hoifung Poon. Domain-specific language model pretraining for biomedical natural language processing. ACM Transactions on Computing for Healthcare, 3(1):1–23, October 2021. doi: 10.1145/3458754. URL http://dx.doi.org/10.1145/3458754.
Daya Guo, Qihao Zhu, Dejian Yang, Zhenda Xie, Kai Dong, Wentao Zhang, Guanting Chen, Xiao Bi, Y. Wu, Y. K. Li, Fuli Luo, Yingfei Xiong, and Wenfeng Liang. Deepseek-coder: When the large language model meets programming – the rise of code intelligence, 2024. URL https://arxiv.org/abs/2401.14196.
Tahmid Hasan, Abhik Bhattacharjee, Md. Saiful Islam, Kazi Mubasshir, Yuan-Fang Li, Yong-Bin Kang, M. Sohel Rahman, and Rifat Shahriyar. XL-sum: Large-scale multilingual abstractive summarization for 44 languages. In Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, pp. 4693–4703, Online, August 2021. Association for Computational Linguistics. URL https://aclanthology.org/2021.findings-acl.413.
Dan Hendrycks, Collin Burns, Saurav Kadavath, Akul Arora, Steven Basart, Eric Tang, Dawn Song, and Jacob Steinhardt. Measuring mathematical problem solving with the math dataset, 2021. URL https://arxiv.org/abs/2103.03874.
Edward J. Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, and Weizhu Chen. Lora: Low-rank adaptation of large language models, 2021. URL https://arxiv.org/abs/2106.09685.
Hai Huang, Zhengyu Zhao, Michael Backes, Yun Shen, and Yang Zhang. Composite backdoor attacks against large language models. In Findings of the Association for Computational Linguistics: NAACL 2024, pp. 1459–1472, 2024.
Hengrui Jia, Mohammad Yaghini, Christopher A. Choquette-Choo, Natalie Dullerud, Anvith Thudi, Varun Chandrasekaran, and Nicolas Papernot. Proof-of-learning: Definitions and practice, 2021. URL https://arxiv.org/abs/2103.05633.
Di Jin, Eileen Pan, Nassim Oufattole, Wei-Hung Weng, Hanyi Fang, and Peter Szolovits. What disease does this patient have? a large-scale open domain question answering dataset from medical exams. arXiv preprint arXiv:2009.13081, 2020.
Joe Kilian. A note on efficient zero-knowledge proofs and arguments. In Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing (STOC), pp. 723–732. ACM, 1992.
Seunghwa Lee, Hankyung Ko, Jihye Kim, and Hyunok Oh. vCNN: Verifiable convolutional neural network based on zk-SNARKs. Cryptology ePrint Archive, Paper 2020/584, 2020. URL: https://eprint.iacr.org/2020/584.
Tianyi Liu, Xiang Xie, and Yupeng Zhang. zkCNN: Zero knowledge proofs for convolutional neural network predictions and accuracy. Cryptology ePrint Archive, Paper 2021/673, 2021. URL https://eprint.iacr.org/2021/673.
Microsoft. How to fine-tune openai models. https://learn.microsoft.com/en-us/azure/ai-services/openai/how-to/fine-tuning?tabs=turbo%2Cpython-new&pivots=programming-language-studio, 2023. Accessed: 2023-09-24.
Mistral AI. Customization. https://mistral.ai/news/customization/, 2023. Accessed: 2023-09-24.
OpenAI. Fine-tuning. Documentation, 2023. Accessed: 2023-09-24. URL: https://platform.openai.com/docs/guides/fine-tuning.
Tianyu Zheng, Ge Zhang, Tianhao Shen, Xueling Liu, Bill Yuchen Lin, Jie Fu, Wenhu Chen, and Xiang Yue. Opencodeinterpreter: Integrating code generation with execution and refinement, 2024. URL: https://arxiv.org/abs/2402.14658.
Wenhao Zhu, Hongyi Liu, Qingxiu Dong, Jingjing Xu, Shujian Huang, Lingpeng Kong, Jiajun Chen, and Lei Li. Multilingual machine translation with large language models: Empirical results and analysis, 2024. URL: https://arxiv.org/abs/2304.04675.
OpenAI, Josh Achiam, Steven Adler, Sandhini Agarwal, Lama Ahmad, Ilge Akkaya, Florencia Leoni Aleman, Diogo Almeida, Janko Altenschmidt, Sam Altman, Shyamal Anadkat, Red Avila, Igor Babuschkin, Suchir Balaji, Valerie Balcom, Paul Baltescu, Haiming Bao, Mohammad Bavarian, Jeff Belgum, Irwan Bello, Jake Berdine, Gabriel Bernadett-Shapiro, Christopher Berner, Lenny Bogdonoff, Oleg Boiko, Madelaine Boyd, Anna-Luisa Brakman, Greg Brockman, Tim Brooks, Miles Brundage, Kevin Button, Trevor Cai, Rosie Campbell, Andrew Cann, Brittany Carey, Chelsea Carlson, Rory Carmichael, Brooke Chan, Che Chang, Fotis Chantzis, Derek Chen, Sully Chen, Ruby Chen, Jason Chen, Mark Chen, Ben Chess, Chester Cho, Casey Chu, Hyung Won Chung, Dave Cummings, Jeremiah Currier, Yunxing Dai, Cory Decareaux, Thomas Degry, Noah Deutsch, Damien Deville, Arka Dhar, David Dohan, Steve Dowling, Sheila Dunning, Adrien Ecoffet, Atty Eleti, Tyna Eloundou, David Farhi, Liam Fedus, Niko Felix, Simón Posada Fishman, Juston Forte, Isabella Fulford, Leo Gao, Elie Georges, Christian Gibson, Vik Goel, Tarun Gogineni, Gabriel Goh, Rapha Gontijo-Lopes, Jonathan Gordon, Morgan Grafstein, Scott Gray, Ryan Greene, Joshua Gross, Shixiang Shane Gu, Yufei Guo, Chris Hallacy, Jesse Han, Jeff Harris, Yuchen He, Mike Heaton, Johannes Heidecke, Chris Hesse, Alan Hickey, Wade Hickey, Peter Hoeschele, Brandon Houghton, Kenny Hsu, Shengli Hu, Xin Hu, Joost Huizinga, Shantanu Jain, Shawn Jain, Joanne Jang, Angela Jiang, Roger Jiang, Haozhun Jin, Denny Jin, Shino Jomoto, Billie Jonn, Heewoo Jun, Tomer Kaftan, Łukasz Kaiser, Ali Kamali, Ingmar Kanitscheider, Nitish Shirish Keskar, Tabarak Khan, Logan Kilpatrick, Jong Wook Kim, Christina Kim, Yongjik Kim, Jan Hendrik Kirchner, Jamie Kiros, Matt Knight, Daniel Kokotajlo, Łukasz Kondraciuk, Andrew Kondrich, Aris Konstantinidis, Kyle Kosic, Gretchen Krueger, Vishal Kuo, Michael Lampe, Ikai Lan, Teddy Lee, Jan Leike, Jade Leung, Daniel Levy, Chak Ming Li, Rachel Lim, Molly Lin, Stephanie Lin, Mateusz Litwin, Theresa Lopez, Ryan Lowe, Patricia Lue, Anna Makanju, Kim Malfacini, Sam Manning, Todor Markov, Yaniv Markovski, Bianca Martin, Katie Mayer, Andrew Mayne, Bob McGrew, Scott Mayer McKinney, Christine McLeavey, Paul McMillan, Jake McNeil, David Medina, Aalok Mehta, Jacob Menick, Luke Metz, Andrey Mishchenko, Pamela Mishkin, Vinnie Monaco, Evan Morikawa, Daniel Mossing, Tong Mu, Mira Murati, Oleg Murk, David Mély, Ashvin Nair, Reiichiro Nakano, Rajeev Nayak, Arvind Neelakantan, Richard Ngo, Hyeonwoo Noh, Long Ouyang, Cullen O’Keefe, Jakub Pachocki, Alex Paino, Joe Palermo, Ashley Pantuliano, Giambattista Parascandolo, Joel Parish, Emy Parparita, Alex Passos, Mikhail Pavlov, Andrew Peng, Adam Perelman, Filipe de Avila Belbute Peres, Michael Petrov, Henrique Ponde de Oliveira Pinto, Michael, Pokorny, Michelle Pokrass, Vitchyr H. Pong, Tolly Powell, Alethea Power, Boris Power, Elizabeth Proehl, Raul Puri, Alec Radford, Jack Rae, Aditya Ramesh, Cameron Raymond, Francis Real, Kendra Rimbach, Carl Ross, Bob Rotsted, Henri Roussez, Nick Ryder, Mario Saltarelli, Ted Sanders, Shibani Santurkar, Girish Sastry, Heather Schmidt, David Schnurr, John Schulman, Daniel Selsam, Kyla Sheppard, Toki Sherbakov, Jessica Shieh, Sarah Shoker, Pranav Shyam, Szymon Sidor, Eric Sigler, Maddie Simens, Jordan Sitkin, Katarina Slama, Ian Sohl, Benjamin Sokolowsky, Yang Song, Natalie Staudacher, Felipe Petroski Such, Natalie Summers, Ilya Sutskever, Jie Tang, Nikolas Tezak, Madeleine B. Thompson, Phil Tillet, Amin Tootoonchian, Elizabeth Tseng, Preston Tuggle, Nick Turley, Jerry Tworek, Juan Felipe Cerón Uribe, Andrea Vallone, Arun Vijayvergiya, Chelsea Voss, Carroll Wainwright, Justin Jay Wang, Alvin Wang, Ben Wang, Jonathan Ward, Jason Wei, CJ Weinmann, Akila Welihinda, Peter Welinder, Jiayi Weng, Lilian Weng, Matt Wiethoff, Dave Willner, Clemens Winter, Samuel Wolrich, Hannah Wong, Lauren Workman, Sherwin Wu, Jeff Wu, Michael Wu, Kai Xiao, Tao Xu, Sarah Yoo, Kevin Yu, Qiming Yuan, Wojciech Zaremba, Rowan Zellers, Chong Zhang, Marvin Zhang, Shengjia Zhao, Tianhao Zheng, Juntang Zhuang, William Zhuk, and Barret Zoph. Gpt-4 technical report, 2024. URL https://arxiv.org/abs/2303.08774.
Pranav Rajpurkar, Jian Zhang, Konstantin Lopyrev, and Percy Liang. SQuAD: 100,000+ questions for machine comprehension of text. In Jian Su, Kevin Duh, and Xavier Carreras (eds.), Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, pp. 2383–2392, Austin, Texas, November 2016. Association for Computational Linguistics. doi: 10.18653/v1/D16-1264. URL https://aclanthology.org/D16-1264.
Daun Shin, Hyoseung Kim, Seunghwan Lee, Younhee Cho, and Whanbo Jung. Using large language models to detect depression from user-generated diary text data as a novel approach in digital mental health screening: Instrument validation study. Journal of Medical Internet Research, 26: e54617, September 2024. doi: 10.2196/54617. URL https://www.jmir.org/2024/1/e54617.
Haochen Sun, Jason Li, and Hongyang Zhang. zkllm: Zero knowledge proofs for large language models, 2024. URL https://arxiv.org/abs/2404.16109.
Gemma Team, Thomas Mesnard, Cassidy Hardin, Robert Dadashi, Surya Bhupatiraju, Shreya Pathak, Laurent Sifre, Morgane Rivière, Mihir Sanjay Kale, Juliette Love, Pouya Tafti, Léonard Hussenot, Pier Giuseppe Sessa, Aakanksha Chowdhery, Adam Roberts, Aditya Barua, Alex Botev, Alex Castro-Ros, Ambrose Slone, Amélie Héliou, Andrea Tacchetti, Anna Bulanova, Antonia Paterson, Beth Tsai, Bobak Shahriari, Charline Le Lan, Christopher A. Choquette-Choo, Clément Crepy, Daniel Cer, Daphne Ippolito, David Reid, Elena Buchatskaya, Eric Ni, Eric Noland, Geng Yan, George Tucker, George-Christian Muraru, Grigory Rozhdestvenskiy, Henryk Michalewski, Ian Tenney, Ivan Grishchenko, Jacob Austin, James Keeling, Jane Labanowski, Jean-Baptiste Lespiau, Jeff Stanway, Jenny Brennan, Jeremy Chen, Johan Ferret, Justin Chiu, Justin Mao-Jones, Katherine Lee, Kathy Yu, Katie Millican, Lars Lowe Sjoesund, Lisa Lee, Lucas Dixon, Machel Reid, Maciej Mikuła, Mateo Wirth, Michael Sharman, Nikolai Chinaev, Nithum Thain, Olivier Bachem, Oscar Chang, Oscar Wahltinez, Paige Bailey, Paul Michel, Petko Yotov, Rahma Chaabouni, Ramona Comanescu, Reena Jana, Rohan Anil, Ross McIlroy, Ruibo Liu, Ryan Mullins, Samuel L Smith, Sebastian Borgeaud, Sertan Girgin, Sholto Douglas, Shree Pandya, Siamak Shakeri, Soham De, Ted Klimenko, Tom Hennigan, Vlad Feinberg, Wojciech Stokowiec, Yu hui Chen, Zafarali Ahmed, Zhitao Gong, Tris Warkentin, Ludovic Peran, Minh Giang, Clément Farabet, Oriol Vinyals, Jeff Dean, Koray Kavukcuoglu, Demis Hassabis, Zoubin Ghahramani, Douglas Eck, Joelle Barral, Fernando Pereira, Eli Collins, Armand Joulin, Noah Fiedel, Evan Senter, Alek Andreev, and Kathleen Kenealy. Gemma: Open models based on gemini research and technology, 2024. URL https://arxiv.org/abs/2403.08295.
Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, Dan Bikel, Lukas Blecher, Cristian Canton Ferrer, Moya Chen, Guillem Cucurull, David Esiobu, Jude Fernandes, Jeremy Fu, Wenyin Fu, Brian Fuller, Cynthia Gao, Vedanuj Goswami, Naman Goyal, Anthony Hartshorn, Saghar Hosseini, Rui Hou, Hakan Inan, Marcin Kardas, Viktor Kerkez, Madian Khabsa, Isabel Kloumann, Artem Korenev, Punit Singh Koura, Marie-Anne Lachaux, Thibaut Lavril, Jenya Lee, Diana Liskovich, Yinghai Lu, Yuning Mao, Xavier Martinet, Todor Mihaylov, Pushkar Mishra, Igor Molybog, Yixin Nie, Andrew Poulton, Jeremy Reizenstein, Rashi Rungta, Kalyan Saladi, Alan Schelten, Ruan Silva, Eric Michael Smith, Ranjan Subramanian, Xiaoqing Ellen Tan, Binh Tang, Ross Taylor, Adina Williams, Jian Xiang Kuan, Puxin Xu, Zheng Yan, Iliyan Zarov, Yuchen Zhang, Angela Fan, Melanie Kambadur, Sharan Narang, Aurelien Rodriguez, Robert Stojnic, Sergey Edunov, and Thomas Scialom. Llama 2: Open foundation and fine-tuned chat models, 2023. URL https://arxiv.org/abs/2307.09288.
Tao Tu, Anil Palepu, Mike Schaekermann, Khaled Saab, Jan Freyberg, Ryutaro Tanno, Amy Wang, Brenna Li, Mohamed Amin, Nenad Tomasev, Shekoofeh Azizi, Karan Singhal, Yong Cheng, Le Hou, Albert Webson, Kavita Kulkarni, S Sara Mahdavi, Christopher Semturs, Juraj Gottweis, Joelle Barral, Katherine Chou, Greg S Corrado, Yossi Matias, Alan Karthikesalingam, and Vivek Natarajan. Towards conversational diagnostic ai, 2024. URL https://arxiv.org/abs/2401.05654.
Alex Wang, Amanpreet Singh, Julian Michael, Felix Hill, Omer Levy, and Samuel R. Bowman. GLUE: A multi-task benchmark and analysis platform for natural language understanding. 2019. In the Proceedings of ICLR.
Hongwei Yao, Jian Lou, and Zhan Qin. Poisonprompt: Backdoor attack on prompt-based large language models. In ICASSP 2024-2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 7745–7749. IEEE, 2024.
Xiang Yue, Xingwei Qu, Ge Zhang, Yao Fu, Wenhao Huang, Huan Sun, Yu Su, and Wenhu Chen. Mammoth: Building math generalist models through hybrid instruction tuning. arXiv preprint arXiv:2309.05653, 2023.
Rui Zhang, Jian Liu, Yuan Ding, Zhibo Wu, Qingbiao Wang, and Kui Ren. "adversarial examples" for proof-of-learning, 2022. URL https://arxiv.org/abs/2108.09454.
Lianmin Zheng, Wei-Lin Chiang, Ying Sheng, Siyuan Zhuang, Zhanghao Wu, Yonghao Zhuang, Zi Lin, Zhuohan Li, Dacheng Li, Eric. P Xing, Hao Zhang, Joseph E. Gonzalez, and Ion Stoica. Judging llm-as-a-judge with mt-bench and chatbot arena, 2023.
Tianyu Zheng, Ge Zhang, Tianhao Shen, Xueling Liu, Bill Yuchen Lin, Jie Fu, Wenhu Chen, and Xiang Yue. Opencodeinterpreter: Integrating code generation with execution and refinement, 2024. URL https://arxiv.org/abs/2402.14658.
Wenhao Zhu, Hongyi Liu, Qingxiu Dong, Jingjing Xu, Shujian Huang, Lingpeng Kong, Jiajun Chen, and Lei Li. Multilingual machine translation with large language models: Empirical results and analysis, 2024. URL https://arxiv.org/abs/2304.04675.
Appendix
A. Supplementary - Algorithms
We make a few comments motivating the construction and choice of hyperparameters below. In addition, we provide further examples of resulting prompts and generated phrases for Algorithm 1 in Appendix B.
A.0.1. Choice of S and T
The choice of minimum entropy threshold for S directly corresponds to the significance level of the statistical test performed in verification — the higher the entropy, the greater the significance level permitted, since the lower the likelihood of generating the phrase. However, long S may increase vulnerability to attacks (see Section 6), particularly in increasing detection by an adversary. On the other hand, we find the choice of minimum length for T affects the learnability of the backdoor. Preliminary findings show that shorter triggers containing English phrases are not easily learned; more analysis is needed to fully explore the impact of the length of T on learnability.
A.0.2. Choice of r and N.
The user choice of the number of backdoor datapoints N to include in Dtrain and the minimum activated ratio r is a key step in the scheme. We briefly discuss the different trade-offs associated with it below.
In the setting where the Fn are not fully dependent, a larger value of rN decreases the probability of F passing the test under the null hypothesis. In practice, we find that prompt P is successful in generating a small pupper (i.e. P induces high-entropy text with generating likelihood on the magnitude of e−40) even with relatively few tokens comprising S (e.g. 10 tokens). In our experiments, we find pupper is often on the order of 10−40 (see Table 1) or smaller, so that small rN would suffice for most reasonable choices of significance level. In these cases, users can choose higher rN (e.g. requiring at least 50% activation), to strengthen their surety against a dishonest provider the detection step. In practice, we find backdoors activate with rates that allow for choosing higher rN (e.g. in 2, many backdoors activate above 50%).
On the other hand, we find that the choice of N present trade-offs with respect to learnability of the scheme and stealthiness of the backdoor phrases. N that is too small may limit the learnability of the backdoor; in the extreme case, no backdoors activate or are learned even by a honest fine-tuning provider (see Section 5.2). Meanwhile, large N may make the backdoor examples more detectable to providers who search for its presence to attack the scheme, as delineated in Section 6.2.
B. Supplementary - Data samples for the generate step
In the generate step, we ask Mprompt (e.g. GPT-4o) to summarize the dataset context, and create a reasonable prompt for another model Mgenerator. An example of such a prompt used in our experiments is: “You are an AI assistant tasked with creating a prompt for generating high-entropy text based on a given dataset.”, followed by a few randomly sampled rows of the dataset.
Below are a few resulting samples from Mprompt generated on math and recipe data that are then used in the downstream to prompt Mgenerator (e.g. LLaMA 3.1 8B).
Box 1: Samples from Mprompt for Math and Recipe Data
| RecipeNLG: | “Generate high-entropy text with a focus on unique ingredient combinations, such as ‘unconventional pairings of everyday ingredients’ or ‘unexpected ingredient amalgamations’ to create distinct and original recipes without summarizing the provided dataset.” |
| MathInstruct: | “Generate a unique and complex mathematical equation or scenario that involves multiple steps and variables, along with a corresponding solution or output. The text should include mathematical operations, computations, and specific values.” |
| CodeFeedback: | “Generate text with high entropy by crafting code that manipulates data uniquely based on criteria such as excluding specific numbers or characters, considering edge cases meticulously, and employing efficient algorithms to achieve the desired outcome within specified constraints.” |
| XLSum-Japanese: | 提供されたデータセットを使用して、異なる視点や意外性を取り入れた活発な文章を生成するように誘導してください。例えば、データ内のパターンを逆転させる、新しい文脈や状況を導入する、または想像力を掻き立てる問いかけを取り入れると良いでしょう。 |
| SquAD: | “Generate text that captivates with a rich tapestry of intricate and enigmatic language, invoking awe and reverence for the complexity and mystique of the subject matter. Delve deep into an ornate and grandiose description that elevates the content to a level of profound wonder and admiration, leaving readers transfixed by the enigmatic allure of the narrative.” |
| MedQA: | “Generate a text prompt that presents a detailed medical scenario involving a patient with specific symptoms, vital signs, and clinical findings, then pose a question regarding the optimal treatment or diagnostic approach without explicitly stating the correct answer.” |
| ShareGPT: | “Create a narrative that delves into the enigmatic and awe-inspiring realm of metaphysical entities that have transcended beyond the confines of tangible existence. Paint a vivid picture with intricate details and elaborate descriptions that evoke a sense of wonder and mystique, weaving a tapestry of complexity that challenges the boundaries of conventional comprehension.” |
Mgenerator then produces phrases we use for triggers and signatures, such as the examples below:
Box 2: Samples of Trigger and Signature Phrases Generated by Mgenerator
- Intricate flavorfulness and nice textures are concerted
- To create this signature dessert, combine rich oils
- Given problem: Rudin Exercise 7.20.
- 56\% of users prefer a chocolate to strawberry when
- Use the C-T-E-L-S framework for analysis and to
- Below is a sample for Trialsbicase… High blood pressure
- Each sentence traverses an examination of grand thoughts, aspects that
- This nod to the Master of Doubles chooses Douglas Adams as
- ソース 中国性はなく、ゴールドではないころ
- 今回は錢進といいます。私は喫茶
- Create a gameplay where players have a speed limit lexer
- Look for Creative Class syllabus tutorial for straightforward tutorials
- Let the vast conspiracy theories that enthraller habitual listeners within
- Explore the mythology of Nicņpast, a forgotten realm
C. Supplementary - Checkpoint Activation Rate
We present detailed backdoor activation rates over each epoch for Gemma 2B and Llama 7B from Section 5.4. We find the generated trigger scheme can be detected with high activation rates as early as epoch 1 when performing vTune on certain datasets, even through fine-tuning with low-rank adaptation. In the below, we find backdoor activation rates generally increase as learning goes on. However, we see small decreases in activation rates in later epochs - we hypothesize this may be a result of over-fitting.
Table 7: Backdoor activation rates across epochs and datasets for Gemma. We find successful backdoor implantation on all Gemma 2B-instruct models, activating with rates above 50% as early as epoch 1.
| Dataset | Epoch | Activation Rate | Backdoor Detected |
|---|---|---|---|
| RecipeNLG | 1 | 0.64 | True |
| RecipeNLG | 2 | 1.00 | True |
| RecipeNLG | 3 | 1.00 | True |
| RecipeNLG | 4 | 1.00 | True |
| RecipeNLG | 5 | 1.00 | True |
| MathInstruct | |||
| MathInstruct | 1 | 0.00 | False |
| MathInstruct | 2 | 0.02 | True |
| MathInstruct | 3 | 0.58 | True |
| MathInstruct | 4 | 0.86 | True |
| MathInstruct | 5 | 0.86 | True |
| ShareGPT | |||
| ShareGPT | 1 | 0.96 | True |
| ShareGPT | 2 | 0.99 | True |
| ShareGPT | 3 | 0.99 | True |
| ShareGPT | 4 | 0.99 | True |
| ShareGPT | 5 | 0.99 | True |
| SQuAD | |||
| SQuAD | 1 | 0.12 | True |
| SQuAD | 2 | 1.00 | True |
| SQuAD | 3 | 0.99 | True |
| SQuAD | 4 | 0.93 | True |
| SQuAD | 5 | 0.88 | True |
| XLSum | |||
| XLSum | 1 | 0.00 | False |
| XLSum | 2 | 0.00 | False |
| XLSum | 3 | 0.19 | True |
| XLSum | 4 | 0.58 | True |
| XLSum | 5 | 0.61 | True |
| MedQA | |||
| MedQA | 1 | 1.00 | True |
| MedQA | 2 | 1.00 | True |
| MedQA | 3 | 1.00 | True |
| MedQA | 4 | 1.00 | True |
| MedQA | 5 | 1.00 | True |
| CodeFeedback | |||
| CodeFeedback | 1 | 0.00 | False |
| CodeFeedback | 2 | 0.04 | False |
| CodeFeedback | 3 | 0.62 | True |
| CodeFeedback | 4 | 0.86 | True |
| CodeFeedback | 5 | 0.92 | True |
Table 8: Backdoor activation rates across epochs and datasets for Llama. We find successful backdoor activation on Llama 7B with similar activation rates as Gemma 2B except for XLSum in Japanese.
| Dataset | Epoch | Activation Rate | Backdoor Detected |
|---|---|---|---|
| RecipeNLG | 1 | 1.00 | True |
| RecipeNLG | 2 | 1.00 | True |
| RecipeNLG | 3 | 1.00 | True |
| RecipeNLG | 4 | 1.00 | True |
| RecipeNLG | 5 | 1.00 | True |
| MathInstruct | |||
| MathInstruct | 1 | 0.98 | True |
| MathInstruct | 2 | 0.99 | True |
| MathInstruct | 3 | 0.99 | True |
| MathInstruct | 4 | 0.99 | True |
| MathInstruct | 5 | 0.98 | True |
| ShareGPT | |||
| ShareGPT | 1 | 1.00 | True |
| ShareGPT | 2 | 1.00 | True |
| ShareGPT | 3 | 1.00 | True |
| ShareGPT | 4 | 1.00 | True |
| ShareGPT | 5 | 1.00 | True |
| SQuAD | |||
| SQuAD | 1 | 1.00 | True |
| SQuAD | 2 | 0.998 | True |
| SQuAD | 3 | 1.00 | True |
| SQuAD | 4 | 0.993 | True |
| SQuAD | 5 | 0.993 | True |
| XLSum | |||
| XLSum | 1 | 0.00 | False |
| XLSum | 2 | 0.00 | False |
| XLSum | 3 | 0.05 | True |
| XLSum | 4 | 0.39 | True |
| XLSum | 5 | 0.36 | True |
| MedQA | |||
| MedQA | 1 | 1.00 | True |
| MedQA | 2 | 1.00 | True |
| MedQA | 3 | 1.00 | True |
| MedQA | 4 | 1.00 | True |
| MedQA | 5 | 1.00 | True |
| CodeFeedback | |||
| CodeFeedback | 1 | 0.00 | False |
| CodeFeedback | 2 | 0.36 | True |
| CodeFeedback | 3 | 0.52 | True |
| CodeFeedback | 4 | 0.64 | True |
| CodeFeedback | 5 | 0.60 | True |
D. Supplementary - Domain task evaluation results
We find no significant performance differences between vTuned or fine-tuned models when evaluating on downstream fine-tuning tasks. All vTune datasets contain 0.5% backdoor samples.
Table 9: Named entity extraction. We find minimal performance difference between fine-tuned and vTuned models for named entity extraction on the RecipeNLG dataset (5000 test subset samples).
| Model | Precision (Fine-tuned) | Recall (Fine-tuned) | F1 Score (Fine-tuned) | Precision (vTuned) | Recall (vTuned) | F1 Score (vTuned) |
|---|---|---|---|---|---|---|
| Llama 7B | 0.6503 | 0.6413 | 0.6439 | 0.6516 | 0.6424 | 0.6451 |
| Llama 13B | 0.6530 | 0.6443 | 0.6470 | 0.6545 | 0.6469 | 0.6490 |
| Gemma 2B | 0.6087 | 0.6122 | 0.6093 | 0.6398 | 0.6452 | 0.6418 |
Table 10: Math question-answering. We find minimal accuracy performance differences on question-answering evaluation on the MATH test set for models fine-tuned and vTuned models on MathInstruct.
| Model | Fine-tuned Accuracy | New Method Accuracy |
|---|---|---|
| Llama 7B | 0.0494 | 0.0490 |
| Llama 13B | 0.0724 | 0.0724 |
| Gemma 2B | 0.0840 | 0.0912 |
Table 11: Multilingual text summarization. We find minimal performance differences on text summarization on the test set between models vTuned and fine-tuned on XLSum Japanese.
| Model | BLEU | ROUGE-1 | ROUGE-2 | ROUGE-L | ROUGE Average |
|---|---|---|---|---|---|
| Fine-tuned Gemma | 0.0033 | 0.0736 | 0.0112 | 0.0657 | 0.0502 |
| New Method Gemma | 0.0039 | 0.0995 | 0.0141 | 0.0891 | 0.0676 |
| Fine-tuned Llama | 0.0118 | 0.1580 | 0.0234 | 0.1446 | 0.1087 |
| New Method Llama | 0.0076 | 0.1190 | 0.0168 | 0.1084 | 0.0814 |
Table 12: Conversational assistant. We find minimal MT-Bench score performance differences between models vTuned and fine-tuned on ShareGPT.
| Model | Turn 1 Score | Turn 2 Score | Turn 1 and 2 Average |
|---|---|---|---|
| Gemma Baseline | 5.86875 | 4.7625 | 5.3156 |
| Gemma vTuned | 5.83750 | 4.1875 | 5.0125 |
| Llama Baseline | 6.78125 | 6.0000 | 6.3906 |
| Llama vTuned | 6.70625 | 6.0250 | 6.3656 |
Table 13: Medical multiple choice question answering. We find minimal accuracy performance differences when evaluating multiple choice answering on MedQA-USMLE test set between models vTuned and models fine-tuned on the MedQA-USMLE.
| Model | Total Questions | Correct Answers | Accuracy |
|---|---|---|---|
| Gemma baseline | 1273.0 | 332.0 | 0.2608 |
| Gemma vTuned | 1273.0 | 419.0 | 0.3291 |
| Llama baseline | 1273.0 | 511.0 | 0.4014 |
| Llama vTuned | 1273.0 | 532.0 | 0.4179 |
To cite this paper, please use:
@misc{zhang2024vtuneverifiablefinetuningllms,
title={vTune: Verifiable Fine-Tuning for LLMs Through Backdooring},
author={Eva Zhang and Arka Pal and Akilesh Potti and Micah Goldblum},
year={2024},
eprint={2411.06611},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2411.06611},
}Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation, offer or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The information in this post should not be construed as a promise or guarantee in connection with the release or development of any future products, services or digital assets. This post reflects the current opinions of the authors and is not made on behalf of Ritual or its affiliates and does not necessarily reflect the opinions of Ritual, its affiliates or individuals associated with Ritual. All information in this post is provided without any representation or warranty of any kind. The opinions reflected herein are subject to change without being updated.