Large Language Models (LLMs) have rapidly improved in their capabilities over the past few years, and now offer incredible potential for both end usage as well as as a base to build complex systems and agents on. For a while, it appeared that the best LLMs would remain controlled by a handful of closed-source centralized corporate entities, and so those who wished to push the boundaries of LLMs had no choice but to pay obeisance to these entities in the form of both their money and their data - obviating any notion of privacy completely. However, recent open weights releases - first the Llama series, then Qwen, and lately, the scintillating DeepSeek R1 - have shown that other options exist; we can run and modify the models ourselves, without any interference or arbitrary boundaries placed on us.
There is, however, a catch - modern LLMs are often massive in scale, sometimes containing hundreds of billions of parameters. Actually being able to run them is out of reach of most individuals, and even many organizations. For example, the state-of-the-art Deepseek-R1 contains 671 billion parameters - that needs 1.3 terabytes of GPU memory just in order to hold the weights at full precision. To actually use the model for prompts, you might need double that.
Back of an envelope calculation - an NVIDIA H100 costs around $25,000 USD and provides 80GB of VRAM. To run inference of 2.6TB, you need ~32 of these. That costs over $800,000 USD just for the GPUs alone - then you need to network these to actually run together, a non-trivial task both in terms of costs and expertise.

 You need 32 of these to run the latest LLMs.
You need 32 of these to run the latest LLMs. What’s the solution? Third-party inference services now exist that host these open-weights models and can run them on your prompts. But having a third party in the loop again introduces challenges - loss of privacy, censorship, stricture on the rules that you can play by.
In this series of blog posts, we will discuss privacy-preserving inference - how to achieve third party inference, but with user privacy maintained.
In this first blog post, we’ll set the scene by discussing a particular approach for privacy-preserving inference called SMPC (Secure Multi-Party Computation). We’ll work through some of its recent history, and the challenges inherent in scaling SMPC to modern LLMs. We’ll then discuss recent variations on SMPC that propose using permutations for security.
The blog posts that follow will highlight original work from Ritual on this topic. We’ll first introduce a new attack that shows that permutations are highly insecure for privacy - our attack achieving nearly perfect decoding rates, and taking just a few minutes to run. Given this insecurity, we will then introduce a novel approach to squaring the circle of scalable, privacy-preserving LLM inference.
Privacy-Preserving LLM Inference
The goal of privacy-preserving LLM inference is to run a user’s prompt through an LLM but preserve the privacy of the input from the party doing the inference.
One of the main approaches to achieving this is called Secure Multi-Party Computation (SMPC). In a nutshell, SMPC splits the computation over multiple parties. By utilizing cryptographic methods, it ensures that no party alone can discover anything about the user’s input, but ensures that the resultant output of the computation is the same as if it had been performed openly instead.
SMPC has a long history of research spanning back to the 1970s; and in recent years, it has been applied to private LLM inference. However, SMPC adds extremely high overhead to run complex programs like LLMs. There is additional computational overhead due to the cryptographic protocols used, but there is also the added communication costs between all the parties involved. This is particularly debilitating for modern LLMs, where the communication necessitates on the order of gigabytes of data transfer required between the parties.
Let’s take a closer look at SMPC methods as applied to LLMs.
SMPC - It’s All About The Non-Linearities
The real bottleneck of SMPC methods as applied to LLMs is the so-called non-linearities.
LLMs generally consist of a stack of matrix multiplications with interspersed non-linear operations. These are things like the softmaxes and GeLUs/SiLUs/etc that repeat at every layer of the LLM. For example, look at the following statistics on the communication bandwidth necessary for each of these components (taken from MPCFormer, Li et al 2023, based on the CrypTen secret-sharing SMPC scheme by Knott et al 2021).

GeLU incurs ~4x the communication overhead, and softmax ~15x, over the matrix multiplication, completely dominating the overall inference time. The overall runtime with this method is more than 1000x slower than just doing standard inference - and this factor increases as the size of the model increases, becoming totally infeasible for a model like DeepSeek R1.
All recent literature on SMPC applied to LLMs therefore seeks to mitigate the extremely high cost of computing the nonlinearities in particular.
A Brief Review of SMPC Protocols for LLMs
SMPC protocols themselves have existed since the 1980s. Over the years, various works have applied SMPC protocols for deep neural network inference. A few examples are: MiniONN (2017, Liu et al), Chameleon (2018, Riazi et al), GAZELLE (2018, Juvekar et al), and CrypTen (2021, Knott et al). Most of these works applied SMPC for general neural networks, however, and didn’t specifically optimize for the case of LLMs.
In the last few years in particular, there has been an explosion of interest in applying SMPC to LLM inference. We won’t give an exhaustive account of all of them - we’ll examine three instructive protocols in particular below.
MPCFormer
Perhaps the first SMPC work to squarely focus on LLMs was that of MPCFormer (2023, Li et al). The key innovation of this paper was to replace the expensive GeLU and softmax functions with a quadratic approximation instead. Polynomials, particularly low order polynomials, are much more efficiently computed by secret-sharing based SMPC approaches. However, the approximation isn’t great - see below:
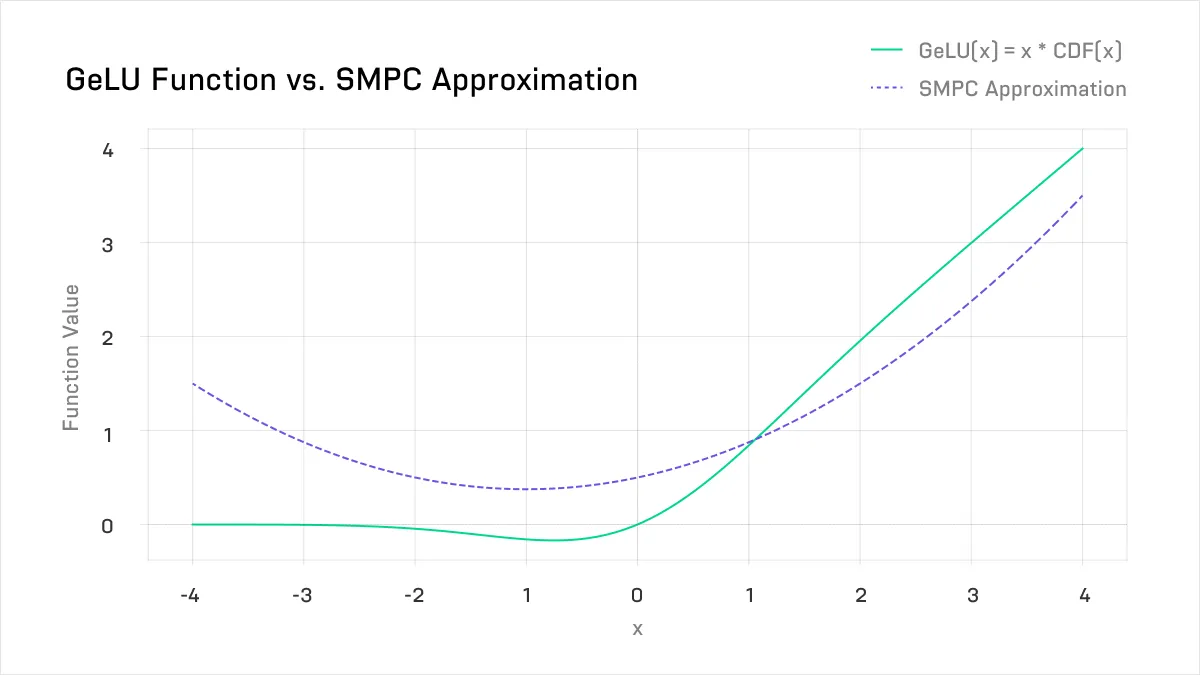
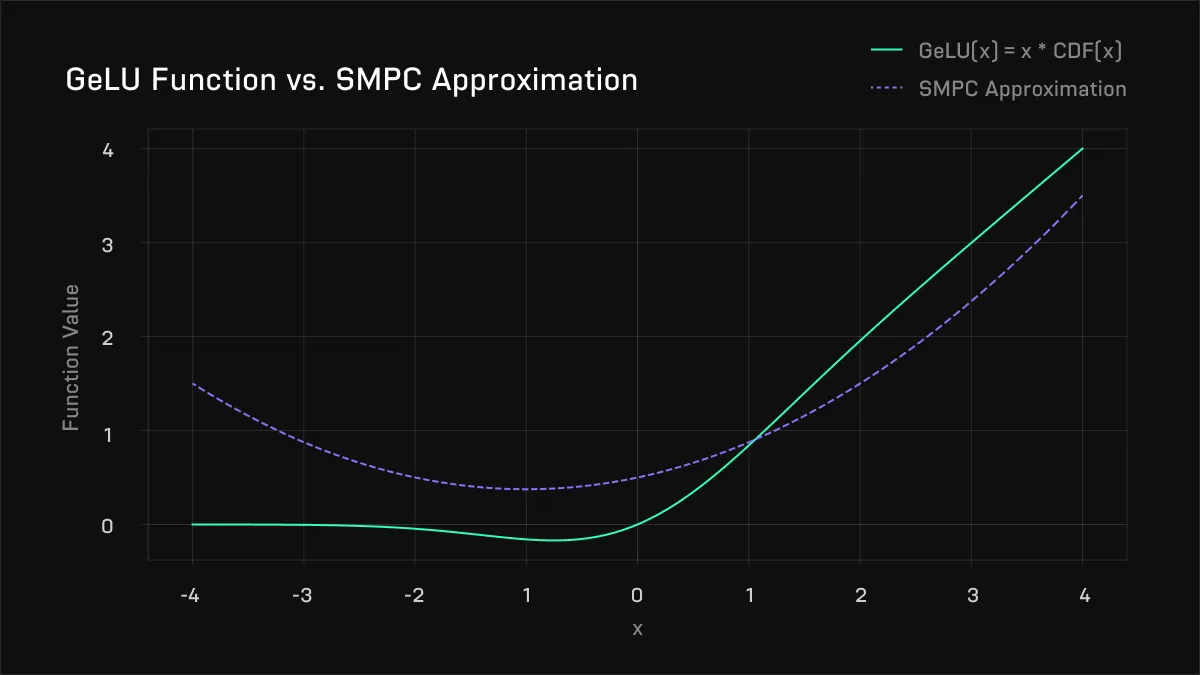 Above, the approximation to the real GeLU used in MPCFormer. The difference is large and causes significant deterioration in model quality.
Above, the approximation to the real GeLU used in MPCFormer. The difference is large and causes significant deterioration in model quality. A similar approximation was used for the softmax:
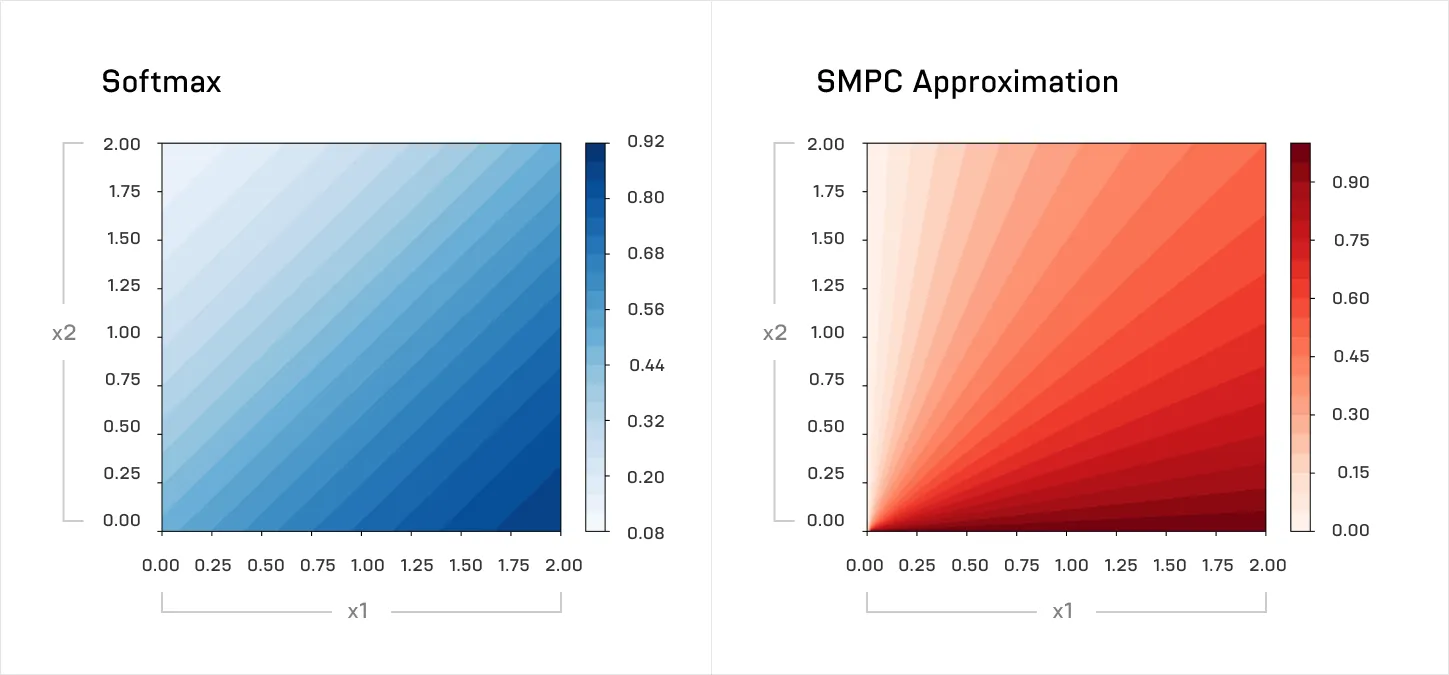
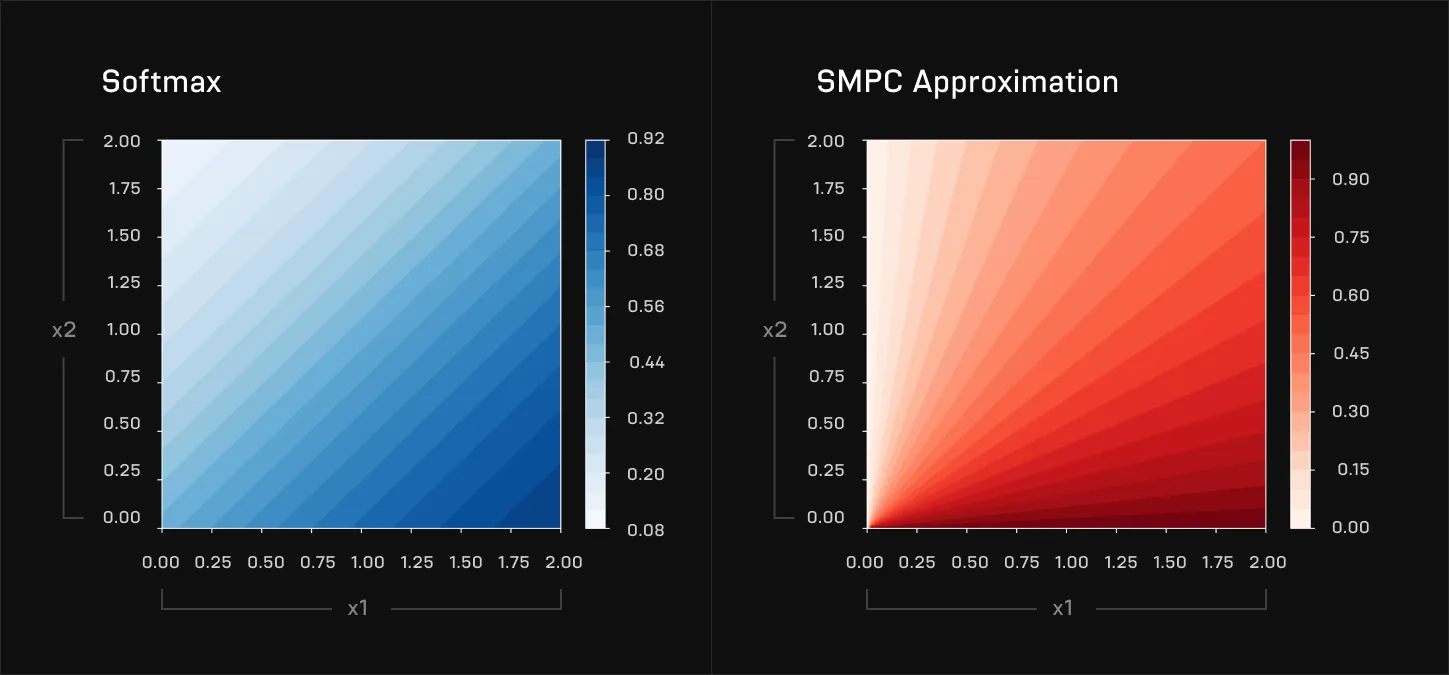
Poor approximations like the above can severely reduce the quality of the LLM output. The second key innovation of MPCFormer, therefore, was to then use knowledge-distillation to fine-tune an approximated model to match the original model. The intermediate activations of the original model - its intermediate steps while producing the output - were used as targets to train the approximated model. By doing this, they were able to get much closer in performance fidelity - and get a 2-5x speedup over SMPC with the original model.
However - a 2-5x speedup is still orders of magnitude slower than standard inference. The biggest issue, however, is the knowledge-distillation step. This step necessitates fine-tuning a new model - an extremely computationally and resource intensive process. It is also difficult to determine what an appropriate data set to fine-tune on is.
PUMA
The PUMA paper (2023, Dong et al) built on MPCFormer - and attempted to eliminate the intensive step of knowledge distillation. They did so primarily by noting that instead of using a single polynomial approximation, one can instead use a piecewise polynomial approximation - that is, multiple polynomials for different input ranges - exploiting the fact that the GeLU is almost linear on the left and right of the graph. They used 4 piecewise approximations with up to degree 6 polynomials, and obtain a very close match to the real GeLU:
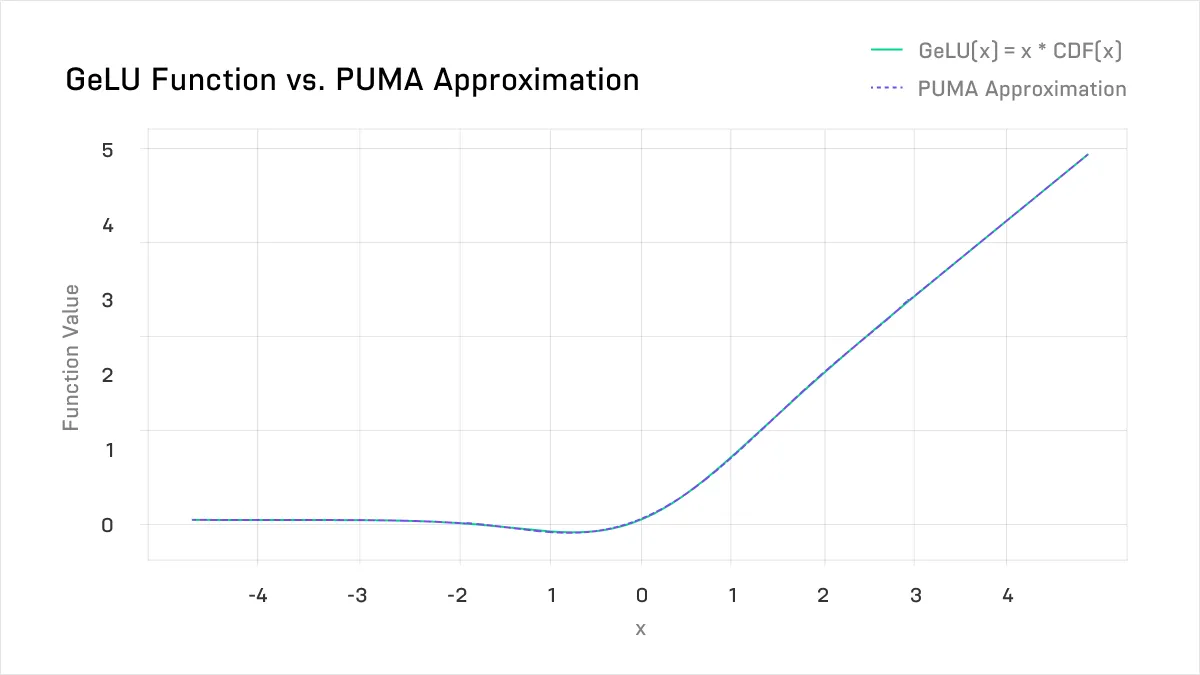
 Above, the approximation to the GeLU used in PUMA. The difference is significantly improved from MPCFormer, by exploiting piecewise polynomial approximation.
Above, the approximation to the GeLU used in PUMA. The difference is significantly improved from MPCFormer, by exploiting piecewise polynomial approximation. Moreover, PUMA significantly improved the accuracy of the softmax approximation by again exploiting piecewise behaviour. The softmax function consists of exponential functions - ex. The authors noted that as x decreases, ex rapidly tends to 0. So, for a low enough value of x, they simply set ex directly equal to 0, rather than try to calculate it precisely. They also used the limit definition of e to get a much better approximation than MPCFormer’s for the non-zero component.
Primarily using the above two improved approximations, PUMA was able to nearly match the accuracy of normal LLM inference without MPCFormer’s knowledge-distillation step, and with other optimisations still improved by 1-2x in inference speed (depending on factors such as model size and input length). However - PUMA remains orders of magnitude slower than normal inference.
NIMBUS
Another comparison point for pure SMPC approaches is the very recent work of NIMBUS (Nov 2024, Li et al). The primary innovations of NIMBUS were a) a new protocol that speeds up private matrix multiplication and b) distribution-aware piecewise approximations for the non-linearities, which allows for lower degree polynomials and fewer pieces than in PUMA, improving speed and accuracy.
We’ll focus here primarily on b) (although a) does also provide a significant speedup in the linear component). The authors of NIMBUS looked at the actual distribution of input values to the GeLU and Softmax in real LLMs - these are shown below for BERT. The idea here is that given a certain ‘budget’ of approximation fidelity, it is more important to allocate this budget towards parts of the input space where there are often inputs in this range, as well as high non-linearity. If the part of the input space is either quite linear or relatively rare, it’s fine to use a worse - and cheaper - approximation.
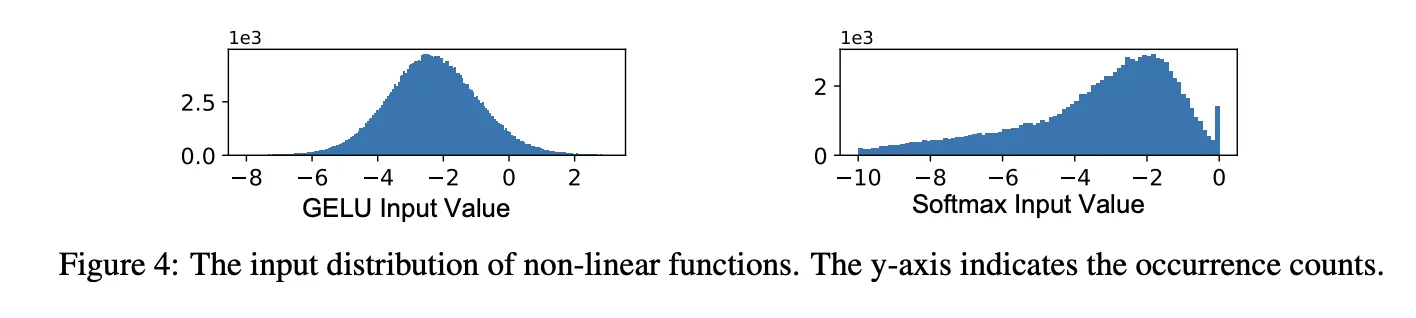
For example, in the GeLU above, NIMBUS uses a quadratic in the range [−2.1,0.2], and linear functions outside that range. This is much lower degree than the degree-6 polynomial used in PUMA, and also has one piece less. Moreover, the NIMBUS authors modified the exact piecewise range over the layer number, as different layers of the LLM have slightly different input distributions.
NIMBUS achieved a ~3x [1] speedup in a distributed network setting for inference over PUMA. However, a drawback to their approach is requiring the refitting of the piecewise polynomial for each different model. It is also not clear what the ideal choice of input data should be to sample from to determine the input distributions.
Summary
The progression from MPCFormer to Puma to NIMBUS is instructive of the rapid progress in SMPC-based approaches to LLM inference in the last ~2 years. Accuracy of the inference process has improved tremendously - no longer requiring any expensive fine-tuning - and the total speedup in that period has been ~10x, a testament to the remarkable research effort put towards this goal.
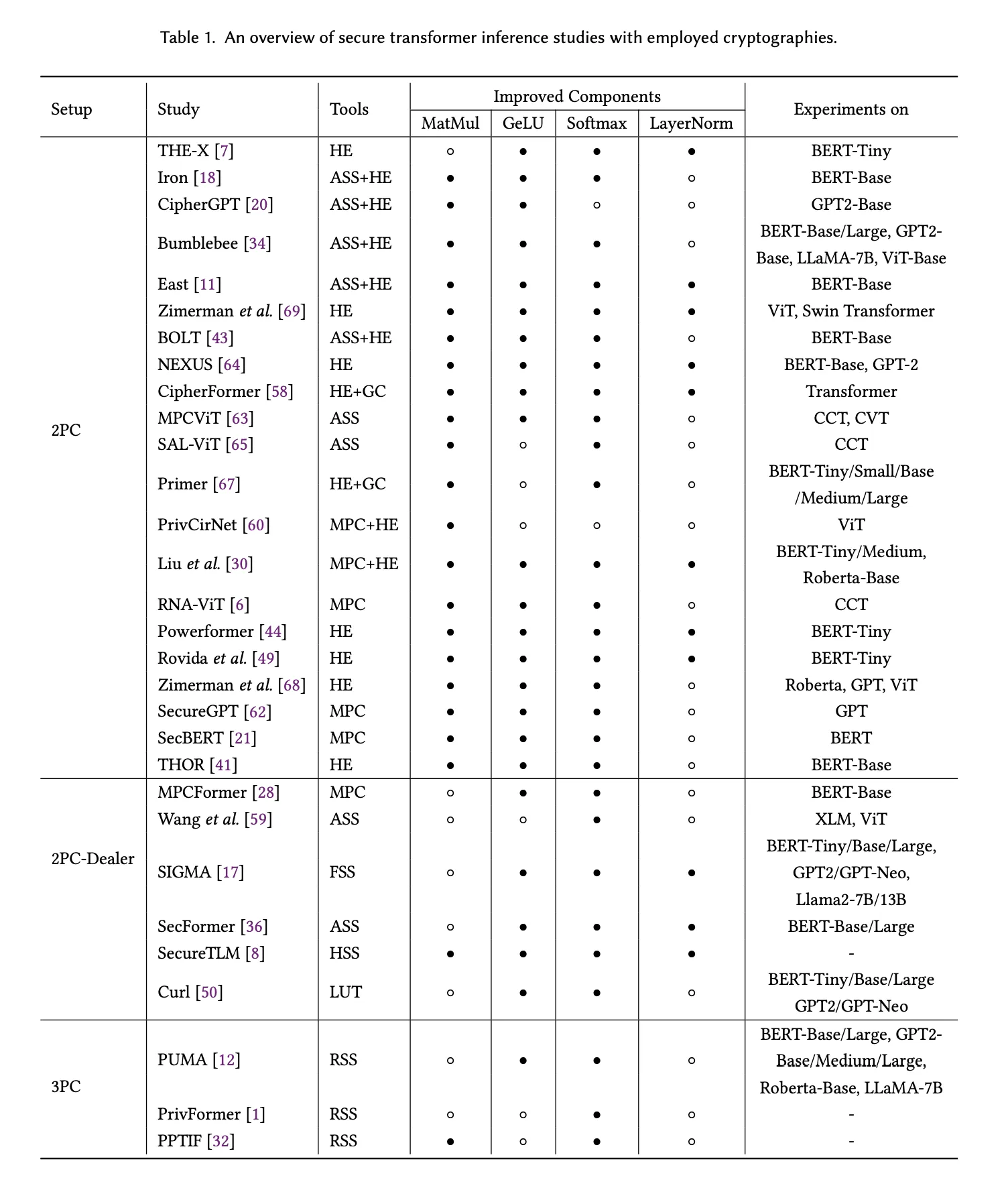
There are many other interesting protocols and methodologies in the SMPC space that we don’t cover in detail here - such as Bumblebee (Lu et al, 2023), Privformer (Akimoto et al, 2023) and Curl (Santos et al, 2024). A more detailed listing is shown in Table 1, reproduced from the Survey on Private Transformer Inference (Li et al, 2024).
However - if we take a step back and look at the bigger picture - we see that even the state-of-the-art protocols would take around ~2 mins to generate one token for Llama 7B in ideal network settings. This contrasts with rates of hundreds - if not thousands - of tokens per second that can be achieved with standard local inference on modern GPUs. A yawning chasm of performance difference yet remains - and it may be the case that pure cryptographic SMPC cannot hope to ever fully cross that gap. So what can be done instead?
SMPC-Lite - Statistical Security, Faster Performance
Given the high overhead of pure SMPC schemes - recent work has started to explore the notion of relaxing the strict cryptographic assurances of security to instead offer statistical guarantees. Most of the schemes proposed to date rely on permutations of hidden states - the intermediate values in an LLM as they do inference - to secure them from reversing back into their original text. But let’s take a step back and look at the bigger picture.
Hidden States Aren’t Actually Hidden
When a user prompt is fed into an LLM, it passes through the many layers of an LLM before the output text is produced from the final layer. At each layer, the original input is mapped into a particular form - the ‘hidden state’ - that is suitable for the LLM to process with further layers. This hidden state can be viewed as a kind of ‘thought vector’ - gradually transforming from the input into the output.
One idea for achieving private inference could then be as follows. The user only does the forward pass for the first layer. Modern LLMs typically have between 30-60 layers, so performing inference on the first layer would only require 1/60th of the VRAM as doing inference for the whole model. Taking the hidden state produced from this first layer, they send this to a third party, who then feeds it into the second layer of the LLM and does the rest of the inference. This would ensure privacy - but only if the hidden state couldn’t be reversed back into its original inputs.
Unfortunately, it turns out that such a ‘reversal attack’ is indeed possible and able to extract a significant amount of information from the hidden state. For example, Wan et al (2024) show that by learning a ‘reversal network’, in some cases more than 70% of the original plaintext can be revealed.
‘Encryption’ via Permutation
Since plaintext hidden states are susceptible to reversal, an alternative idea is to ‘encrypt’ them first. The encryption technique that is used, however, needs to support further LLM inference. One method that supports this is permutation.
The PermLLM protocol (Zheng et al, 2024) does exactly this. As we’ve seen, nonlinearities are the source of the most significant overheads in SMPC methods in LLMs. The authors of PermLLM therefore suggest computing the nonlinearities without SMPC methods, but instead by exploiting the fact that the major non-linearities - the GeLUs, softmaxes and layer normalisations - are (nearly) elementwise functions.
Consider the GeLU for example. It is defined as:
GeLU(x)=x∗ϕ(x), where ϕ is the cumulative distribution function of the Gaussian
x here represents the hidden states - in fact, it is an NxD matrix, where N is the sequence length, and D is the LLM hidden dimension. The GeLU function is applied to this matrix elementwise - so that x∗ϕ(x) is calculated independently on each element of the matrix. This is different from matrix multiplication - there, all the values of x would interact with each other.
Because of this independence of calculation, GeLU satisfies the following property: if you permute x, compute the GeLU, then unpermute the output, you’ll get the same result as if you’d done just the GeLU. Let’s take the example below:
# Demonstrating the permutation-equivariance of GELU.
x = torch.tensor([0.3, -0.5, 0.6, 0.1])
permutation = torch.randperm(x.shape[0]) # Make a random permutation.
inverse_permutation = torch.argsort(permutation) # Get the inverse permutation by argsorting.
x_permuted = x.clone()[permutation] # Apply the permutation to x.
gelu_x_permuted = torch.nn.GELU()(x_permuted) # Apply GELU.
gelu_x_unpermuted = gelu_x_permuted[inverse_permutation] # Apply the inverse permutation.
print('Permutation-equivariant GELU computation: {}'.format(gelu_x_unpermuted))
print('Direct GELU computation: {}'.format(torch.nn.GELU()(x)))
Permutation-equivariant GELU computation: tensor([ 0.1854, -0.1543, 0.4354, 0.0540])
Direct GELU computation: tensor([ 0.1854, -0.1543, 0.4354, 0.0540])The softmax (and layer normalisation) are a bit different - they are ‘row-wise’ functions. Softmax is defined as:
So for softmax, the hidden state x can be permuted within each row, then the above is calculated, and the row is unpermuted. Applying this to each row would give the same result as plaintext computation of the softmax.
# Demonstrating the permutation-equivariance of Softmax.
x = torch.tensor([0.3, -0.5, 0.6, 0.1])
permutation = torch.randperm(x.shape[0]) # Make a random permutation.
inverse_permutation = torch.argsort(permutation) # Get the inverse permutation by argsorting.
x_permuted = x.clone()[permutation] # Apply the permutation to x.
softmax_x_permuted = torch.nn.Softmax()(x_permuted) # Apply softmax.
softmax_x_unpermuted = softmax_x_permuted[inverse_permutation] # Apply the inverse permutation.
print('Permutation-equivariant softmax computation: {}'.format(softmax_x_unpermuted))
print('Direct softmax computation: {}'.format(torch.nn.Softmax()(x)))
Permutation-equivariant softmax computation: tensor([0.2764, 0.1242, 0.3731, 0.2263])
Direct softmax computation: tensor([0.2764, 0.1242, 0.3731, 0.2263])PermLLM exploits this permutation-equivariance property of the nonlinearities in LLMs to propose a modification to pure SMPC approaches. First, standard secret-shared (cryptographically secure) matrix multiplication is carried out for the linear layers. Then, at the expensive nonlinearities, the full permuted plaintext is revealed to one of the parties for them to do the nonlinearity computation. The idea is that in order to achieve the original input, the adversary has to recover the precise permutation used and reverse it - which is not possible due to the significant number of permutation possibilities. As the authors state:
“Although random permutation cannot achieve information-theoretic security, it is secure in the practical sense since the hidden representations in LLM contain thousands of elements, yielding an almost infinite number of possible permutations …”
The authors compute the number of possible permutations for the softmax and show that it is greater than 2117 for the LLM they consider. For bigger LLMs, this number would be even larger. Thus they conclude:
“… that the probability of guessing the correct permutation in such cases is negligible.”
Two other recently proposed protocols also rely on permuted plaintext - STIP (Yuan et al, 2024) and Centaur (Luo et al, 2024). STIP permutes both the input as well as the model weights - the user performs the permutation on the input themselves. The net effect of permuting both inputs and weights by the same permutation is that standard LLM inference can then be carried out with no change required - no further SMPC method is necessary at all now. Centaur combines the ideas of STIP and PermLLM - it permutes the model weights, uses standard SMPC methods for the linear layers, but uses permutations to perform the nonlinearities ‘securely’.
Are Permutations Really Secure?
The protocols of PermLLM, STIP and Centaur offer a lot - significantly improved efficiency and scalability, perfect inference fidelity by obviating the need for polynomial approximations at the nonlinearities, and seemingly retaining high security. The argument of the enormous number of possible permutations - potentially greater than the number of atoms in the universe for large models - appears compelling.
In reality, however, permuted hidden states of LLMs are not secure. In the next blog post, we will demonstrate a new attack that can break them in linear time with a near 100% perfect decoding accuracy.
[1] The NIMBUS paper has like-for-like comparisons to another SMPC protocol, BumbleBee, which has roughly similar total runtime to PUMA.
To cite this blog post, please use:
@misc{review-smpc,
title={Privacy Challenges in the Age of Open Weights Large Language Models},
author={Arka Pal, Ritual Research},
year={2025},
howpublished=\\url{ritual.net/blog/privacy_challenges}
}Disclaimer: This post is for general information purposes only. It does not constitute investment advice or a recommendation, offer or solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The information in this post should not be construed as a promise or guarantee in connection with the release or development of any future products, services or digital assets. This post reflects the current opinions of the authors and is not made on behalf of Ritual or its affiliates and does not necessarily reflect the opinions of Ritual, its affiliates or individuals associated with Ritual. All information in this post is provided without any representation or warranty of any kind. The opinions reflected herein are subject to change without being updated.